
【题目】某公司有A、B、C、D、E五辆汽车,其中A、B两辆汽车的车牌尾号均为1,C、D两辆汽车的车牌尾号均为2,E车的车牌尾号为6.已知在非限行日,每辆车可能出车或不出车,A、B、E三辆汽车每天出车的概率均为 ![]() ,C、D两辆汽车每天出车的概率均为
,C、D两辆汽车每天出车的概率均为 ![]() ,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
例如,星期一禁止车牌尾号为0和5的车辆通行.
(1)求该公司在星期一至少有2辆汽车出车的概率;
(2)设X表示该公司在星期二和星期三两天出车的车辆数之和,求X的分布列及数学期望.
【答案】
(1)解:记事件A“该公司在星期一至少有2辆车出车”,
则P(A)=1﹣ ![]()
![]() ﹣
﹣ ![]()
![]()
![]() ﹣
﹣ ![]()
![]()
![]()
![]()
=1﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]()
= ![]() ;
;
(2)解:根据题意,X的可能取值为0,1,2,3,4,5;
则P(X=0)= ![]()
![]() =
= ![]() ,
,
P(X=1)= ![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]() =
= ![]() ,
,
P(X=2)= ![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]() =
= ![]() ,
,
P(X=3)= ![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]() =
= ![]() ,
,
P(X=4)= ![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]() =
= ![]() ,
,
P(X=5)= ![]()
![]() =
= ![]() ;
;
∴随机变量X的分布列为:
X | 0 | 1 | 2 | 3 | 4 | 5 |
P | | | | | | |
数学期望为E(X)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() +4×
+4× ![]() +5×
+5× ![]() =
= ![]() .
.
【解析】(1)记事件A“该公司在星期一至少有2辆车出车”,利用独立重复试验的概率乘法公式,求解即可;(2)X的可能取值为0,1,2,3,4,5,求出对应的概率,写出分布列,计算数学期望值.
【考点精析】认真审题,首先需要了解离散型随机变量及其分布列(在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列).


科目:高中数学 来源: 题型:
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足4千步为不健康生活方式,不少于16千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为200人,高一学生人数为700人,高二学生人数600人,高三学生人数500,从中抽取n人作为调查对象,得到了如图所示的这n人的频率分布直方图,这n人中有20人被学校界定为不健康生活方式者. 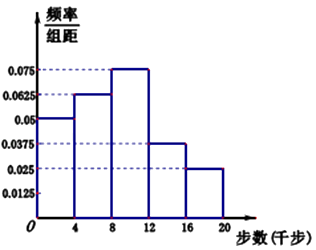
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取3人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励0元,超健康生活方式者表彰奖励20元,一般生活方式者鼓励性奖励10元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三第一学期期末四校联考数学第I卷中共有8道选择题,每道选择题有4个选项,其中只有一个是正确的;评分标准规定:“每题只选一项,答对得5分,不答或答错得0分.”某考生每道题都给出一个答案,已确定有5道题的答案是正确的,而其余选择题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜,试求出该考生:
(1)得40分的概率;
(2)得多少分的可能性最大?
(3)所得分数ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kex﹣x2(其中k∈R,e是自然对数的底数).
(Ⅰ)若k<0,试判断函数f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若k=2,当x∈(0,+∞)时,试比较f(x)与2的大小;
(Ⅲ)若函数f(x)有两个极值点x1 , x2(x1<x2),求k的取值范围,并证明0<f(x1)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知min{{a,b}= ![]() f(x)=min{|x|,|x+t|},函数f(x)的图象关于直线x=﹣
f(x)=min{|x|,|x+t|},函数f(x)的图象关于直线x=﹣ ![]() 对称;若“x∈[1,+∞),ex>2mex”是真命题(这里e是自然对数的底数),则当实数m>0时,函数g(x)=f(x)﹣m零点的个数为 .
对称;若“x∈[1,+∞),ex>2mex”是真命题(这里e是自然对数的底数),则当实数m>0时,函数g(x)=f(x)﹣m零点的个数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(2x+φ)(|φ< ![]() |)的图象向左平移
|)的图象向左平移 ![]() 个单位后关于原点对称,求函数f(x)在[0,
个单位后关于原点对称,求函数f(x)在[0, ![]() ]上的最小值为( )
]上的最小值为( )
A.﹣ ![]()
B.﹣ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以![]() 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,![]() 表示具有如下性质的函数
表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数
,存在一个正数![]() ,使得函数
,使得函数![]() 的值域包含于区间
的值域包含于区间![]() .例如,当
.例如,当![]() ,
,![]() 时,
时,![]() ,
,![]() .现有如下命题:
.现有如下命题:
①设函数![]() 的定义域为
的定义域为![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() ”;
”;
②函数![]() 的充要条件是
的充要条件是![]() 有最大值和最小值;
有最大值和最小值;
③若函数![]() ,
,![]() 的定义域相同,且
的定义域相同,且![]() ,
,![]() ,则
,则![]() ;
;
④若函数![]() (
(![]() ,
,![]() )有最大值,则
)有最大值,则![]() .
.
其中的真命题有 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,焦点在x轴上的椭圆,离心率 ![]() ,且椭圆过点
,且椭圆过点 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)椭圆左,右焦点分别为F1 , F2 , 过F2的直线l与椭圆交于不同的两点A、B,则△F1AB的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com