若曲线C:y=x3-2ax2+2ax上任意点处的切线的倾斜角都为锐角,且a为整数.
(1)求曲线C的解析式;
(2)求过点(1,1)的曲线的切线方程.
【答案】
分析:(1)根据曲线C:y=x
3-2ax
2+2ax上任意点处的切线的倾斜角都为锐角,可得y'=3x
2-4ax+2a>0恒成立,结合a为整数,可求曲线C的解析式;
(2)设出切点坐标,表示出切线方程,利用切点在曲线及切线上,即可求得过点(1,1)的曲线的切线方程.
解答:解:(1)∵曲线C:y=x
3-2ax
2+2ax上任意点处的切线的倾斜角都为锐角
∴y'=3x
2-4ax+2a>0恒成立,
∴△=16a
2-24a<0,
∴
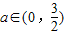
,….(3分)
∵a∈Z,
∴a=1,
∴f(x)=x
3-2x
2+2x…(6分)
(2)令切点为(
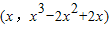
,
∴
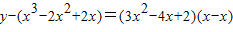
,…(8分)
∵点(1,1)在切线上,
∴
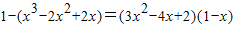
,
∴
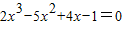
,
∴
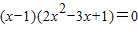
,
∴
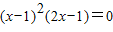
,
∴x
=1或
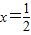
.
∴切线方程为y=x或
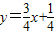
….(12分)
点评:本题以函数为载体,考查导数知识的运用,考查切线的斜率,考查导数的几何意义,应注意区分过点的切线与在点处的切线含义的不同.

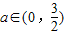 ,….(3分)
,….(3分)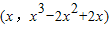 ,
,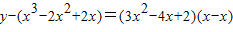 ,…(8分)
,…(8分)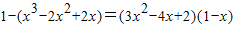 ,
,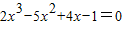 ,
,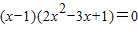 ,
,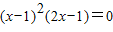 ,
,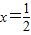 .
.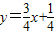 ….(12分)
….(12分)
