
【题目】某工厂对新研发的一种产品进行试销,得到如下数据表:

(1)根据上表求出回归直线方程![]() ,并预测当单价定为8.3元时的销量;
,并预测当单价定为8.3元时的销量;
(2)如果该工厂每件产品的成本为5.5元,利用所求的回归方程,要使得利润最大,单价应该定为多少?
附:线性回归方程![]() 中斜率和截距最小二乘估计计算公式:
中斜率和截距最小二乘估计计算公式:
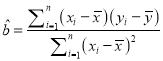 ,
, ![]()
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有![]() ,当
,当![]() 时,有
时,有![]()
(1)求f(1)的值;
(2)判断f(x)的单调性并加以证明;
(3)若f(4)=2,求f(x)在[1,16]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 经过点
经过点![]() 倾斜角为
倾斜角为![]() .(10分).
.(10分).
(1)写出直线![]() 的参数方程
的参数方程
(2)求直线![]() 与直线
与直线![]() 的交点到点
的交点到点![]() 的距离
的距离
(3)设![]() 与圆
与圆![]()
![]() 相交于两点
相交于两点![]() ,求点
,求点![]() 到
到![]() 两点的距离的和与积。
两点的距离的和与积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是中央电视台最近推出的一档有重大影响力的大型电视文化节目,今年两会期间,教育部部长陈宝生答记者问时就给予其高度评价.基于这样的背景,山东某中学积极响应,也举行了一次诗词竞赛.组委会在竞赛后,从中抽取了部分选手的成绩(百分制),作为样本进行统计,作出了图1的频率分布直方图和图2的茎叶图(但中间三行污损,看不清数据).
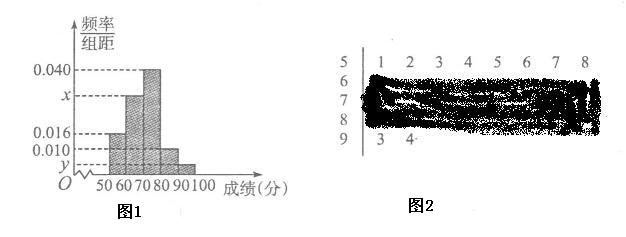
(I)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(II)分数在[80,90)的学生中,男生有2人,现从该组抽取三人“座谈”,写出基本事件空间并求至少有两名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是公差为1的等差数列,a1 , a5 , a25成等比数列.
(1)求数列{an}的通项公式;
(2)设bn= ![]() 3+an , 求数列{bn}的前n项和Tn .
3+an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 斜率大于零的直线
斜率大于零的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,且与其准线交于点
两点,且与其准线交于点![]() .
.

(Ⅰ)若线段![]() 的长为
的长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在点
上是否存在点![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com