【题目】已知向量 
=（sinθ，cosθ﹣2sinθ）， 
=（1，2）．
（1）若 
，求tanθ的值；
（2）若 
，求θ的值．
【答案】
（1）解：∵ 
∥ 
∴2sinθ=cosθ﹣2sinθ即4sinθ=cosθ
∴tanθ= 
（2）解：由| |=| |
∴sin2θ+（cosθ﹣2sinθ）2=5
即1﹣2sin2θ+4sin2θ=5化简得sin2θ+cos2θ=﹣1
故有sin（2θ+ 
）=﹣ 
又∵θ∈（0，π）∴2θ+ ∈（ ， 
π）
∴2θ+ = 
π或2θ+ = 
π
∴θ= 
或θ= 
π
【解析】（1）根据平面向量的共线定理的坐标表示即可解题．（2）由| |=| |化简得sin2θ+cos2θ=﹣1，再由θ∈（0，π）可解出θ的值．
【考点精析】关于本题考查的平面向量的坐标运算，需要了解坐标运算：设
，
则
;
;设
，则
才能得出正确答案．
科目：高中数学 来源： 题型：
【题目】我们国家正处于老龄化阶段，“老有所依”也是政府的民生工程.为了了解老人们的健康状况，政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估，健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级，并以80岁为界限分成两个群体进行统计，样本分布被制作成如图表.
（1）若采用分层抽样的方法，再从样本中不能自理的老人中抽取16人进一步了解他们的生活状况，则两个群体中各应抽取多少人？
（2）据统计该市大约有
的户籍老人无固定收入,且在各健康状况人群中所占比例相同，政府计划每月为这部分老人发放生活补贴，标准如下：
①80岁及以上长者每人每月发放生活补贴200元；
②80岁以下老人每人每月发放生活补贴120元；
③不能自理的老人每人每月额外再发放生活补贴100元.
若用频率估计概率，设任意户籍老人每月享受的生活补贴为
元，求
的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某金匠以黄金为原材料加工一种饰品，经多年的数据统计得知，该金匠平均每加5 个饰品中有4个成品和1个废品，每个成品可获利3万元，每个废品损失1万元，假设该金匠加工每件饰品互不影响，以频率估计概率.
（1）若金金匠加工4个饰品，求其中废品的数量不超过1的概率；
（2）若该金匠加工了 3个饰品，求他所获利润的数学期望.
(两小问的计算结果都用分数表示）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某校高三上学期期末数学考试成绩中，随机抽取了
名学生的成绩得到如图所示的频率分布直方图：
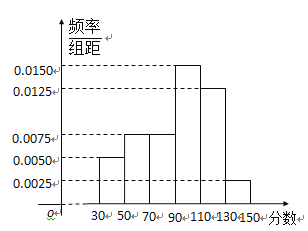
（1）根据频率分布直方图，估计该校高三学生本次数学考试的平均分；
（2）若用分层抽样的方法从分数在
和
的学生中共抽取
人，该人中成绩在的有几人？
（3）在（2）中抽取的人中，随机抽取
人，求分数在和各
人的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，
底面
，底面是直角梯形，
，
，
，
是
上的点．
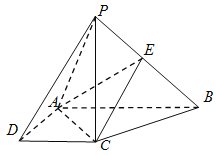
（Ⅰ）求证：平面
⊥平面
；
（Ⅱ）若
是
的中点，且二面角
的余弦值为
，求直线
与平面
所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次数学考试中，第22题和第23题为选做题，规定每位考生必须且只须在其中选做一题，现有甲、乙、丙、丁4名考生参加考试，其中甲、乙选做第22题的概率均为
，丙、丁选做第22题的概率均为
．
(Ⅰ)求在甲选做第22题的条件下，恰有两名考生选做同一道题的概率；
(Ⅱ)设这4名考生中选做第22题的学生个数为X，求X的概率分布及数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
