无穷等差数列{an}的各项均为整数,首项为a1、公差为d,Sn是其前n项和,3、21、15是其中的三项,给出下列命题;
①对任意满足条件的d,存在a1,使得99一定是数列{an}中的一项;
②对任意满足条件的d,存在a1,使得30一定是数列{an}中的一项;
③存在满足条件的数列{an},使得对任意的n∈N*,S2a=4Sn成立.
其中正确命题为 .(写出所有正确命题的序号)
【答案】
分析:利用等差数列的公式,分别讨论前n项和3、21、15的具体项数,然后进行推理即可.首先根据条件得出d≤6;①99-21=78能被6整除,且=13,假设15和21之间有n项,那么99和21之间有13n项,得出结论;②30-21=9不能被6整除,如果d=6,那么30一定不是数列{a
n}中的一项,得出结论.③利用等差数列的前n项和公式化简S
2n=4S
n,得出结论
解答:解:要使等差数列的公差最大,则3,15,21因为相邻的前n项和,此时对应 两项为15-3=12,21-15=6,所以d≤6.
①99-21=78能被6整除,且
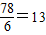
,假设15和21之间有n项,那么99和21之间有13n项,所以99一定是数列{a
n}中的一项,所以①正确.
②30-21=9不能被6整除,如果d=6,那么30一定不是数列{a
n}中的一项,所以②错误.
③如果有S
2n=4S
n,那么由等差数列求和公式有:2na
1+n(2n-1)•d=4[na
1+
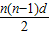
],化简得到,d=2a
1,所以只要满足条件d=2a
1的数列{a
n},就能使得对任意的n∈N
*,S
2n=4S
n成立,所以③正确.
故答案为:①③.
点评:本题考查等差数列的通项公式及前n项和公式的应用,解题的关键是根据条件得出公差.考查学生分析问题,解决问题的能力,综合性较强,难度较大.

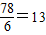 ,假设15和21之间有n项,那么99和21之间有13n项,所以99一定是数列{an}中的一项,所以①正确.
,假设15和21之间有n项,那么99和21之间有13n项,所以99一定是数列{an}中的一项,所以①正确.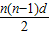 ],化简得到,d=2a1,所以只要满足条件d=2a1的数列{an},就能使得对任意的n∈N*,S2n=4Sn成立,所以③正确.
],化简得到,d=2a1,所以只要满足条件d=2a1的数列{an},就能使得对任意的n∈N*,S2n=4Sn成立,所以③正确.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案