
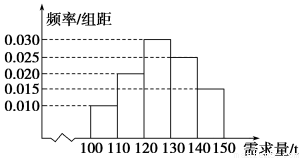
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望.
(1) T=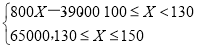 (2)0.7(3) 59400
(2)0.7(3) 59400
【解析】(1)当X∈[100,130)时,
T=500X-300(130-X)=800X-39 000.
当X∈[130,150]时,T=500×130=65 000.
所以T=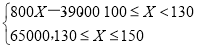
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
(3)依题意可得T的分布列为
T | 45 000 | 53 000 | 61 000 | 65 000 |
P | 0.1 | 0.2 | 0.3 | 0.4 |
所以E(T)=45 000×0.1+53 000×0.2+61 000×0.3+65 000×0.4=59400.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:填空题
在正项数列{an}中,a1=2,an+1=2an+3×5n,则数列{an}的通项公式为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知数列{an}和{bn}满足:a1=λ,an+1=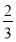 an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
(1)对任意实数λ,证明:数列{an}不是等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:解答题
已知函数f(x)=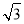 sin2x+sin xcos x,x∈
sin2x+sin xcos x,x∈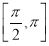 .
.
(1)求f(x) 的零点;
(2)求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:选择题
若M为△ABC所在平面内一点,且满足(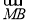 -
-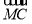 )·(
)·(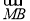 +
+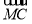 -2
-2 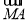 )=0,则△ABC为( ).
)=0,则△ABC为( ).
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:填空题
已知正态分布总体落在区间(-∞,0.3)的概率为0.5,那么相应的正态曲线φμ,σ(x)在x=________时达到最高点.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:解答题
如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.
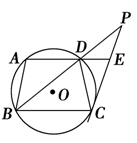
(1)求证:AB2=DE·BC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
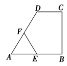
如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=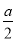 ,点E,F分别为线段AB,AD的中点,则EF=________.
,点E,F分别为线段AB,AD的中点,则EF=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:填空题
已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com