
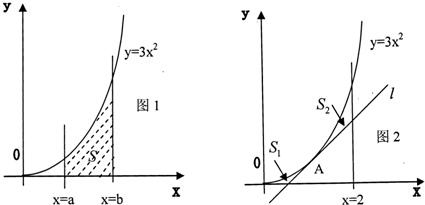
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
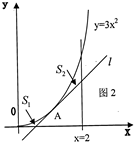 解:设切点A的坐标为(a,3a2),(1分)
解:设切点A的坐标为(a,3a2),(1分)| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 9 |
| 4 |
| 3 |
| 8 |
| 9 |
| 8 |
| 9 |


科目:高中数学 来源: 题型:
如图1,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(0,2),且其面积为8.
(1)求此抛物线的解析式;
(2)如图2,若P点为抛物线上不同于A的一点,连接PB并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为S、R.
①求证:PB=PS;
②判断△SBR的形状;
③试探索在线段SR上是否存在点M,使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似?若存在,请找出M点的位置;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:解答题
如图所示,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点.
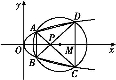
(1)求r的取值范围;
(2)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市学军中学高考数学模拟试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com