
(Ⅰ)求双曲线C的方程;
(Ⅱ)若直线FQ按向量a=(0,1)平移后所得直线与双曲线C交于不同两点M、N,当-![]() ≤
≤![]() ≤-
≤-![]() 时,求直线PQ的斜率的取值范围.
时,求直线PQ的斜率的取值范围.
解:(Ⅰ)设双曲线C的方程为![]() =1(a>0,b>0),
=1(a>0,b>0),
∵右顶点为A(1,0),
∴a=1,∴![]() (其中c=
(其中c=![]() ),
),
∴G点坐标为(![]() ,0).
,0).
设P(x1,y1),Q(x2,y2),则
![]() =(x1-
=(x1-![]() ,y1),
,y1),![]() =(x2-
=(x2-![]() ,y2),
,y2),
![]() =(1-
=(1-![]() ,0),
,0),
∵![]() =0
=0
∴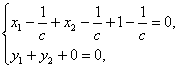
则∴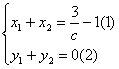
又P、Q在双曲线C上,
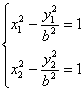 ,作差并整理得,
,作差并整理得,
(x1+x2)(x1-x2)=![]() ③,
③,
∵![]() ≠0,∴x1≠x2.
≠0,∴x1≠x2.
将②代入③得,x1+x2=0,
代入①得0=![]() -1,∴c=3,∴b2=c2-a2=8.
-1,∴c=3,∴b2=c2-a2=8.
∴双曲线C的方程为:x2-![]() =1.
=1.
(Ⅱ)设直线PQ的斜率为k,由(Ⅰ)知直线PQ过原点,
∴直线PQ的方程为:y=kx,代入C:x2-![]() =1并整理得(8-k2)x2=8,
=1并整理得(8-k2)x2=8,
∴8-k2>0,∴k2<8,
直线MN是由直线PQ按a=(0,1)平移得到,故可设直线MN的方程为:y=kx+l,代入C:x2-![]() =1消去y并整理,得(8-k2)x2-2kx-9=0,
=1消去y并整理,得(8-k2)x2-2kx-9=0,
由A=4k2+36(8-k2)=288-32k2>0,
解得k2<9,
故知在k2<8的条件下,直线MN与双曲线总有两个交点.
设这两个交点为M(x3,y3),N(x4,y4),则
x3+x4=![]() ,x3x4=
,x3x4=![]() ,
,
∵y3=kx3+1,y4=kx4+1,
∴y3y4=(kx3+1)(kx4+1)=k2x3x4+k(x3+x4)+1,
∴![]() =(x3,y3)·(x4,y4)=x3x4+y3y4
=(x3,y3)·(x4,y4)=x3x4+y3y4
=(1+k2)x3x4+k(x3+x4)+1
=(1+k2)·![]() +1
+1
=![]() ,
,
由![]() ≤
≤![]() ≤
≤![]() ,得
,得![]() ≤
≤![]() ≤
≤![]() ,
,
由此可知1≤k2≤2![]()
![]() ≤
≤![]() ≤
≤![]() .
.
∴直线PQ的斜率的取值范围为:[![]() ,-1]∪[1,
,-1]∪[1,![]() ].
].


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 已知双曲线C的中心为坐标原点O,焦点F1、F2在x轴上,点P在双曲线的左支上,点M在右准线上,且满足
已知双曲线C的中心为坐标原点O,焦点F1、F2在x轴上,点P在双曲线的左支上,点M在右准线上,且满足| F1O |
| PM |
| OF1 |
| OM |
| 3 |
| B2A |
| B2B |
| B2A |
| B1B |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| FM |
| ME |
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年崇文区一模理)(13分) 已知双曲线C的中心为坐标原点O,焦点F1、F2在x轴上,点P在双曲线的左支上,点
M在右准线上,且满足![]()
(Ⅰ)求双曲线C的离心率e;
(Ⅱ)若双曲线C过点Q(2,![]() ),B1、B2是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且
),B1、B2是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且![]() ,求直线AB的方程.
,求直线AB的方程.

查看答案和解析>>
科目:高中数学 来源:2012年云南省昆明市高三复习适应性检测数学试卷(文科)(解析版) 题型:填空题
 是双曲线C的一个焦点,过点F作渐近线的垂线l,垂足为M,直线l交y轴于点E,若
是双曲线C的一个焦点,过点F作渐近线的垂线l,垂足为M,直线l交y轴于点E,若 ,则C的方程为 .
,则C的方程为 .查看答案和解析>>
科目:高中数学 来源:2007年北京市崇文区高考数学一模试卷(理科)(解析版) 题型:解答题
 .
. ),B1、B2是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且
),B1、B2是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且 ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com