
公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克,当20≤X<80时,认定为酒后驾车;当X≥80时,认定为醉酒驾车,重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中,依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量,酒精含量X(单位:毫克)的统计结果如下表:
| X | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,+∞) |
| 人数 | t | 1 | 1 | 1 | 1 | 1 |
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
下表中有三个游戏规则,袋子中分别装有大小相同的球,从袋子中取球,分别计算甲获胜的概率,说明哪个游戏是公平的?
| 游戏1 | 游戏2 | 游戏3 |
| 1个红球和1个白球 | 2个红球和2个白球 | 3个红球和1个白球 |
| 取1个球 | 取1个球,再取1个球 | 取1个球,再取1个球 |
| 取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
| 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 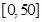 | 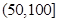 | 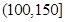 | 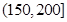 | 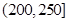 | 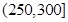 | 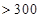 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
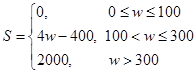 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率; 列联表,并判断能否有
列联表,并判断能否有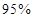 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?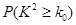 | 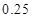 | 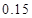 | 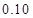 | 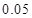 | 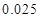 | 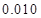 | 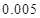 | 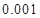 |
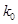 | 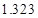 | 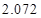 | 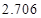 | 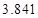 | 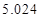 | 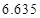 | 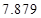 | 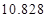 |
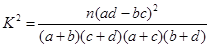
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有7道题,其中5道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的两道题都是甲类题的概率;
(2)所取的两道题不是同一类题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是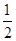 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出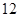 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
| 学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
| 人数 | 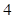 | 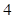 | 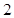 | 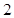 |
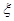 ,求随机变量
,求随机变量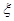 的分布列及数学期望
的分布列及数学期望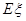 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为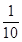 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为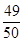 ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱).
(1)求在1次游戏中:
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com