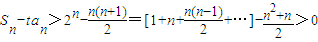设函数y=f(x)的图象是曲线C1,曲线C2与C1关于直线y=x对称.将曲线C2向右平移1个单位得到曲线C3,已知曲线C3是函数y=log2x的图象.
(I)求函数f(x)的解析式;
(II)设an=nf(x)(n∈N*),求数列{an}的前n项和Sn,并求最小的正实数t,使Sn<tan对任意n∈N*都成立.
【答案】
分析:(I)根据函数的图象的平移法则可求曲线C
2的图象,由曲线C
2与曲线C
1关于直线y=x对称,即曲线C
2是函数y=log
2(x+1)的反函数可求
(II)由题设:a
n=n×2
n-n,,利用分组求和及错位相减可求S
n,使S
n<ta
n对任意n∈N
*都成立.即S
n-ta
n<0恒成立,
解答:解:(I)由题意知,曲线C
3向左平移1个单位得到曲线C
2,∴曲线C
2是函数y=log
2(x+1)的图象.…(2分)
曲线C
2与曲线C
1关于直线y=x对称,∴曲线C
2是函数y=log
2(x+1)的反函数的图象y=log
2(x+1)的反函数为y=2
x-1
∴f(x)=2
x-1…(4分)
(II)由题设:a
n=n×2
n-n,n∈N
*S
n=(1×2
1-1)+(2×2
2-2)+(3×2
3-3)+…+(n•2
n-n)=(1×2
1+2×2
2+3×2
2+…+n×2
n)-(1+2+3+…+n)…(6分)=
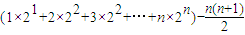
=
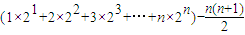
①
2S
n=(1×2
2+2×2
3+3×2
4+…+n×2
n+1)-n(n+1)②
由②-①得,
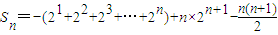
,=
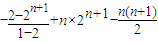
=
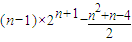
…(8分)
当
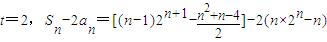
=
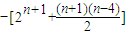
S
1-2a
1=-1<0,S
2-2a
2=-5<0,S
3-2a
3=-14<0
当n≥4时,
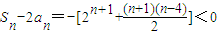
∴当t=2时,对一切n∈N
*,S
n<2a
n恒成立.
当0<t<2时,
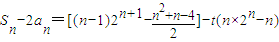
=
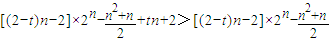
记
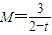
,则当n大于比M大的正整数时,
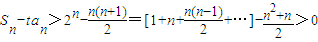
也就证明当t∈(0,2)时,存在正整数n,使得S
n>ta
n.
也就是说当t∈(0,2)时,S
n≤ta
n不可能对一切n∈N
*都成立.∴t的最小值为2.…(14分)
点评:本题以函数的图象的平移变换为切入点,考查了互为反函数的函数解析式的求解,数列的求和的错位相减求和的应用,解答的难点在于试题的计算及逻辑推理

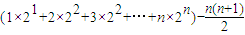 =
=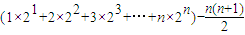 ①
①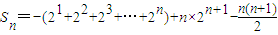
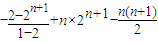 =
=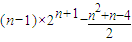 …(8分)
…(8分)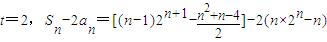 =
=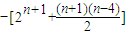 S1-2a1=-1<0,S2-2a2=-5<0,S3-2a3=-14<0
S1-2a1=-1<0,S2-2a2=-5<0,S3-2a3=-14<0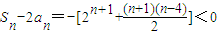 ∴当t=2时,对一切n∈N*,Sn<2an恒成立.
∴当t=2时,对一切n∈N*,Sn<2an恒成立.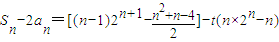 =
=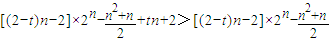
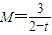 ,则当n大于比M大的正整数时,
,则当n大于比M大的正整数时,