
| A. | 1 | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 在一个棱长为$2\sqrt{6}$的正四面体纸盒内放一个正方体,并且能使正方体在纸盒内任意转动,说明正方体在正四面体的内切球内,求出内切球的直径,就是正方体的对角线的长,然后求出正方体的棱长
解答 解:设球的半径为:r,由正四面体的体积得:
4×$\frac{1}{3}$×r×$\frac{\sqrt{3}}{4}$×($2\sqrt{6}$)2=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$×($2\sqrt{6}$)2×$\sqrt{(2\sqrt{6})^{2}-(\frac{2}{3}•\frac{\sqrt{3}}{2}•2\sqrt{6})^{2}}$,
所以r=1,
设正方体的最大棱长为a,
∴3a2=22,
∴a=$\frac{2\sqrt{3}}{3}$.
故选:B
点评 本题是中档题,考查正四面体的内接球的知识,球的内接正方体的棱长的求法,考查空间想象能力,转化思想,计算能力


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
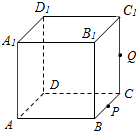 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 0 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com