
分析 (1)由已知可得sin2A+sin2B-sin2C=sinA•sinC.即a2+c2-b2=ac,$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{1}{2}$,可得$B=\frac{π}{3}$.
(2)2a+c=2R(2sinA+sinC)=5sinA+$\sqrt{3}$cosA=2$\sqrt{7}$sin(A+φ)
其中,sinφ=$\frac{\sqrt{3}}{2\sqrt{7}}$,cosφ=$\frac{5}{2\sqrt{7}}$,$φ∈(0,\frac{π}{3})$
由$A+φ∈(φ,\frac{2π}{3}+φ)$,得2$\sqrt{7}$sin(A+φ)∈($\sqrt{3}$,2$\sqrt{7}$].即$2a+c∈(\sqrt{3},2\sqrt{7}]$
解答 解:(1)由cos2B-cos2A=2sinC•(sinA-sinC),可得sin2A+sin2B-sin2C=sinA•sinC.
根据正弦定理得a2+c2-b2=ac,
由余弦定理,得$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{1}{2}$,∵0<B<π,∴$B=\frac{π}{3}$.
(2)由(1)得:2R=$\frac{b}{sinB}=2$,
2a+c=2R(2sinA+sinC)=2[2sinA+sin($\frac{2π}{3}-A$)]=5sinA+$\sqrt{3}$cosA=2$\sqrt{7}$sin(A+φ)
其中,sinφ=$\frac{\sqrt{3}}{2\sqrt{7}}$,cosφ=$\frac{5}{2\sqrt{7}}$,$φ∈(0,\frac{π}{3})$
∵A$∈(0,\frac{2π}{3}$),∴$A+φ∈(φ,\frac{2π}{3}+φ)$,
∴当$A+φ=\frac{π}{2}$时,${(2a+c)_{max}}=2\sqrt{7}$,
当$A+φ=\frac{2π}{3}+φ$时,$(2a+c)=2\sqrt{3}$,
当A+φ=φ时,$(2a+c)=\sqrt{3}$.所以2$\sqrt{7}$sin(A+φ)∈($\sqrt{3}$,2$\sqrt{7}$].
即$2a+c∈(\sqrt{3},2\sqrt{7}]$
点评 本题考查了三角恒等变形,正余弦定理的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
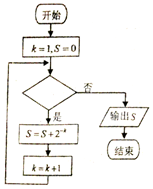
| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com