
(13分)在 中,设
中,设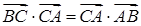 .
.
(1)求证: 为等腰三角形;
为等腰三角形;
(2)若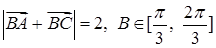 ,求
,求 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
(本小题满分13分)
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从10个样本中随机抽出2名学生的成绩,设选出学生的分数为90分以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和均值.
的分布列和均值.
| 9 | 2 | 8 | 8 |
| 8 | 5 | 5 | |
| 7 | 4 | 4 | 4 |
| 6 | 0 | 0 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三第四次月考文科数学 题型:解答题
.(本小题满分13分)
在数列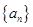 中,
中,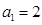 ,
,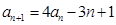 ,
,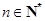 .
.
(1)证明数列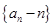 是等比数列;
是等比数列;
(2)设数列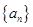 的前
的前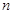 项和
项和 ,求
,求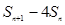 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市丰台区高三下学期统一练习数学理卷 题型:解答题
(本小题共13分)
在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc.
(Ⅰ)求角A的大小;
(Ⅱ)设函数 ,当
,当 取最大值
取最大值 时,判断△ABC的形状.
时,判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分13分)
在△![]() 中,已知
中,已知![]() ·
·![]() =9,sin
=9,sin![]() =cos
=cos![]() sin
sin![]() ,面积S
,面积S![]() =6.
=6.
(Ⅰ)求△![]() 的三边的长;
的三边的长;
(Ⅱ)设![]() 是△
是△![]() (含边界)内一点,
(含边界)内一点,![]() 到三边
到三边![]() ,
,![]() ,
,![]() 的距离分别为x,y和z,求x+y+z的取值范围.
的距离分别为x,y和z,求x+y+z的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com