
若数列 满足
满足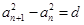 ,其中
,其中 为常数,则称数列
为常数,则称数列 为等方差数列,已知等方差数列
为等方差数列,已知等方差数列 满足
满足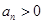 ,
,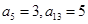 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前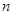 项和;
项和;
(3)记 ,则当实数
,则当实数 大于4时,不等式
大于4时,不等式 能否对于一切的
能否对于一切的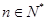 恒成立?请说明理由。
恒成立?请说明理由。
(1)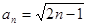 ;(2)
;(2)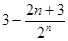 ;(3)当
;(3)当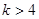 时,不等式
时,不等式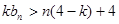 对于一切的
对于一切的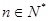 恒成立 .
恒成立 .
【解析】本试题主要考查了数列的概念和灵活运用新的定义,解决数列的通项公式和求和问题,以及不等式的恒成立问题的综合运用
(1)利用新定义可得由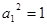 ,
, 得,
得,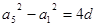 ,∴
,∴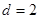
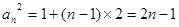
(2)中结合上一问的结论得到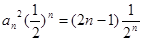 ,然后利用错位相减法得到求和
,然后利用错位相减法得到求和
(3)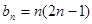 ,不等式
,不等式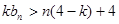 恒成立,
恒成立,
即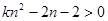 对于一切的
对于一切的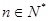 恒成立。
恒成立。
∴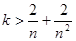
分离参数的思想求解k的取值范围。
解:(Ⅰ)由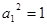 ,
, 得,
得,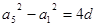 ,∴
,∴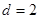
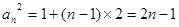 ,
,
∵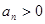 ,∴
,∴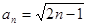
数列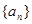 的通项公式为
的通项公式为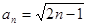 ;
;
(Ⅱ)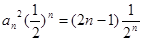
设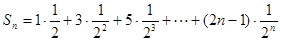 ①
①
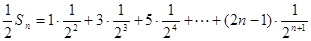 ②
②
①-②,得
∴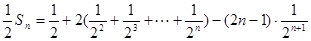
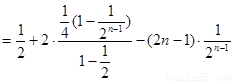
∴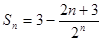
即数列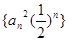 的前
的前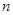 项和为
项和为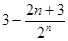
(Ⅲ)解法1: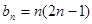 ,不等式
,不等式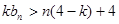 恒成立,
恒成立,
即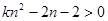 对于一切的
对于一切的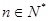 恒成立。
恒成立。
设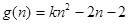 ,当
,当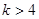 时,由于对称轴
时,由于对称轴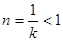 ,且
,且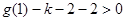
而函数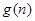 在
在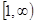 是增函数,∴不等式
是增函数,∴不等式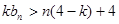 恒成立,
恒成立,
即当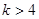 时,不等式
时,不等式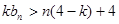 对于一切的
对于一切的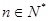 恒成立
恒成立
解法2: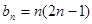 ,不等式
,不等式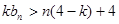 恒成立,即
恒成立,即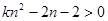 对于一切的
对于一切的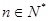 恒成立。
恒成立。
∴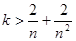
∵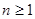 ,∴
,∴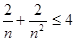 .而
.而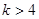
∴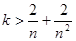 恒成立.
恒成立.
故当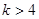 时,不等式
时,不等式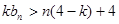 对于一切的
对于一切的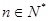 恒成立.
恒成立.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
| an+2 |
| an+1 |
| an+1 |
| an |
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
| n•3n |
| 3n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| sina |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4an-2 |
| an+1 |
| 146 |
| 65 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都外国语学校高三(上)11月月考数学试卷(解析版) 题型:填空题
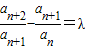 (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列.查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都外国语学校高三(上)11月月考数学试卷(解析版) 题型:填空题
 (λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 .
(λ为常数),则称数列{an}为比等差数列,λ称为比公差.现给出以下命题,其中所有真命题的序号是 . ,则数列{an}是比等差数列,且比公差λ=2;
,则数列{an}是比等差数列,且比公差λ=2; ,a1=2,则此数列的通项为
,a1=2,则此数列的通项为 -1,且{an}不是比等差数列;
-1,且{an}不是比等差数列; ,且an=
,且an= ,则此数列的通项为an=
,则此数列的通项为an= ,且{an}不是比等差数列.
,且{an}不是比等差数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com