
已知曲线C上的动点P(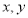 )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为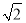
(1)求曲线C的方程。
(2)过点M(1,2)的直线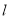 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线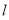 的方程。
的方程。
(1):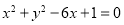 (或
(或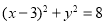 );(2)
);(2)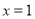 或
或
【解析】
试题分析:(1)根据动点P(x,y)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为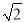 ,建立方程,化简可得曲线C的方程.
,建立方程,化简可得曲线C的方程.
(2)分类讨论,设出直线方程,求出圆心到直线的距离,利用勾股定理,即可求得直线l的方程.
试题解析:(1)由题意得|PA|=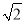 |PB| 2分;
|PB| 2分;
故 3分;
3分;
化简得: (或
(或 )即为所求。 5分;
)即为所求。 5分;
(2)当直线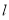 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为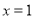 ,
,
将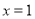 代入方程
代入方程 得
得 ,
,
所以|MN|=4,满足题意。 8分;
当直线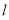 的斜率存在时,设直线
的斜率存在时,设直线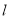 的方程为
的方程为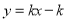 +2
+2
由圆心到直线的距离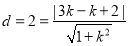 10分;
10分;
解得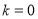 ,此时直线
,此时直线 的方程为
的方程为
综上所述,满足题意的直线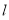 的方程为:
的方程为: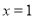 或
或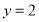 . 12分.
. 12分.
考点:(1)圆的标准方程;(2)点到直线的距离公式.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源:2015届湖北孝感高级中学高二上学期期末考试理科数学试卷(解析版) 题型:选择题
函数y=f(x)在定义域(-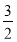 ,3)内的图像如图所示.记y=f(x)的导函数为y=f?(x),则不等式f?(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f?(x),则不等式f?(x)≤0的解集为( )
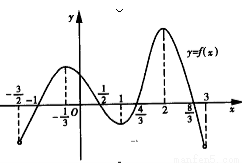
A.[-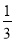 ,1]∪[2,3)
,1]∪[2,3)
B.[-1,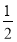 ]∪[
]∪[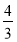 ,
, ]
]
C.[-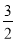 ,
,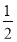 ]∪[1,2)
]∪[1,2)
D.(-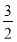 ,-
,-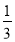 ]∪[
]∪[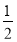 ,
,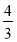 ]∪[
]∪[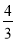 ,3)
,3)
查看答案和解析>>
科目:高中数学 来源:2015届浙江省台州市高二第一学期期末数学试卷(解析版) 题型:选择题
右图是边长相等的两个正方形.给定下列三个命题:

①存在三棱柱,其正视图、侧视图如右图;
②存在四棱柱,其正视图、侧视图如右图;
③存在圆柱,其正视图、侧视图如右图.
其中真命题的个数是
A. 3 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:2015届浙江温州十校联合体高二上学期期末联考理数学卷(解析版) 题型:选择题
设 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,下列四个命题中假命题的是( )
是三个不同的平面,下列四个命题中假命题的是( )
A.若 则
则 B.若
B.若 则
则
C.若 则
则 D.若
D.若 ,则
,则
查看答案和解析>>
科目:高中数学 来源:2015届河南郑州高二上学期期末考试理科数学试卷(解析版) 题型:选择题
抛物线 的焦点F恰好是双曲线
的焦点F恰好是双曲线 的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 ( )
的右焦点,且它们的交点的连线过点F,则双曲线的离心率为 ( )
A.  B.
B.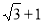 C. 3 D.
C. 3 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com