
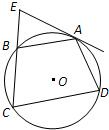
 �����⣺
�����⣺
|
|
| 12 |
| 3cos2��+4sin2�� |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
|
|
|
|
| x2 |
| 4 |
| y2 |
| 3 |
| x |
| yz |
| y |
| zx |
| 1 |
| z |
| x |
| y |
| y |
| x |
| 2 |
| z |
| y |
| zx |
| z |
| xy |
| 2 |
| x |
| z |
| xy |
| x |
| yz |
| 2 |
| y |
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| AB |
| CD |
| BE |
| DA |
|
|
|
|
|
|
|
|
|
|
| x2 |
| 4 |
| y2 |
| 3 |
| |-1-0-2| | ||
|
3
| ||
| 2 |
| |1-0-2| | ||
|
| ||
| 2 |
| 2 |
| x |
| yz |
| y |
| zx |
| 1 |
| z |
| x |
| y |
| y |
| x |
| 2 |
| z |
| y |
| zx |
| z |
| xy |
| 2 |
| x |
| z |
| xy |
| x |
| yz |
| 2 |
| y |
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �����⣺��ѡ���⣺������A��B��C��D�ĸ�С����ֻ��ѡ�����⣩
�����⣺��ѡ���⣺������A��B��C��D�ĸ�С����ֻ��ѡ�����⣩| 5 |
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ�߿���ѧ����Ѻ���Ծ���01���������棩 ���ͣ������
 �����߶�AC�ij��ȣ�
�����߶�AC�ij��ȣ� ������ֵ��2=2����Ӧ��һ����������
������ֵ��2=2����Ӧ��һ���������� ���������A��
���������A�� �����Dz�����������OΪ���㣬x���������Ϊ���ᣬȡ��ֱ������ϵ����ͬ�ĵ�λ���ȣ�����������ϵ��������C�ļ����귽�̣�
�����Dz�����������OΪ���㣬x���������Ϊ���ᣬȡ��ֱ������ϵ����ͬ�ĵ�λ���ȣ�����������ϵ��������C�ļ����귽�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010������ʡ��������һ�и߶���ѧ�����п�����ѧ���ģ� ���ͣ������
(������)��������20��
��ͼ����֪������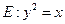
 ��Բ
��Բ �ཻ��A��B��C��D�ĸ��㡣
�ཻ��A��B��C��D�ĸ��㡣
������r��ȡֵ��Χ �����ı���ABCD��������ʱ����Խ���AC��BD�Ľ���P�����ꡣ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com