
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)| 5 |
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
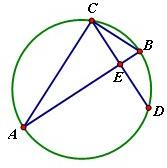 解:A.(选修4-l:几何证明选讲)
解:A.(选修4-l:几何证明选讲)| 5 |
| 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011年吉林省高一上学期期末质量检测数学试卷 题型:解答题
附加题:(本小题10分,实验班同学必做,其他班学生选做)
是否存在常数a,使得函数f (x)=sin2x+acosx+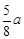 -
-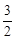 在闭区间
在闭区间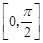 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学仿真押题试卷(01)(解析版) 题型:解答题
 ,求线段AC的长度.
,求线段AC的长度. 和特征值λ2=2及对应的一个特征向量
和特征值λ2=2及对应的一个特征向量 ,试求矩阵A.
,试求矩阵A. (θ是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(θ是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com