
已知曲线C:
(1)当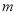 为何值时,曲线C表示圆;
为何值时,曲线C表示圆;
(2)在(1)的条件下,若曲线C与直线 交于M、N两点,且
交于M、N两点,且 ,求
,求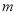 的值.
的值.
(3)在(1)的条件下,设直线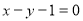 与圆
与圆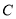 交于
交于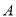 ,
,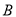 两点,是否存在实数
两点,是否存在实数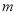 ,使得以
,使得以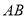 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数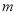 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)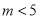 ;(2)
;(2) ;(3)存在实数
;(3)存在实数 使得以
使得以 为直径的圆过原点,
为直径的圆过原点,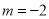 .
.
【解析】
试题分析:(1)二元二次方程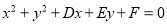 表示圆的充要条件为
表示圆的充要条件为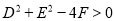 (2)(2)直线和圆相交,根据半径,弦长的一半,圆心距求弦长.(3)圆的弦长的常用求法:(1)几何法:求圆的半径
(2)(2)直线和圆相交,根据半径,弦长的一半,圆心距求弦长.(3)圆的弦长的常用求法:(1)几何法:求圆的半径 ,弦心距
,弦心距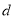 ,弦长
,弦长 ,则
,则 (2)代数方法:运用根与系数的关系及弦长公式
(2)代数方法:运用根与系数的关系及弦长公式 ;(3)与圆有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用直线与圆的位置关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.
;(3)与圆有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用直线与圆的位置关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点.
试题解析:解 :(1)由D2+E2-4F=4+16-4m=20-4m>0,得m<5. 3分
(2)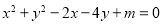 ,即
,即 ,
,
所以圆心C(1,2),半径 , 4分
, 4分
 圆心C(1,2)到直线
圆心C(1,2)到直线 的距离
的距离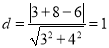 5分
5分
又 ,
, ,即
,即 ,
, . 6分
. 6分
(3)假设存在实数 使得以
使得以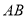 为直径的圆过原点,则
为直径的圆过原点,则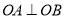 ,设
,设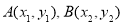 ,则
,则 , 7分
, 7分
由 得
得 , 8分
, 8分
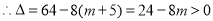 ,即
,即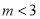 ,又由(1)知
,又由(1)知 ,
,
故 9分
9分
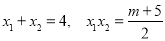 10分
10分
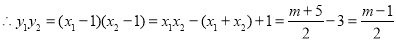 11分
11分
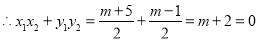
 12分
12分
故存在实数 使得以
使得以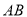 为直径的圆过原点,
为直径的圆过原点,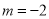 . 13分
. 13分
考点:(1)二元二次方程表示圆的条件;(2)弦长公式的应用;(3)探索性问题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2016届福建省高一下学期第二次阶段考数学试卷(解析版) 题型:选择题
方程x2+y2+2x-4y-6=0表示的图形是( )
A.以(1,-2)为圆心,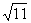 为半径的圆
为半径的圆
B.以(1,2)为圆心,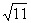 为半径的圆
为半径的圆
C.以(-1,-2)为圆心, 为半径的圆
为半径的圆
D.以(-1,2)为圆心, 为半径的圆
为半径的圆
查看答案和解析>>
科目:高中数学 来源:2016届福建省晋江市高一年下学期期中考试数学试卷(解析版) 题型:填空题
二次函数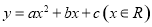 的部分对应值如下表:
的部分对应值如下表:
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| -6 | 0 | 4 | 6 | 6 | 4 | 0 | -6 |
则不等式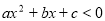 的解集是_______________________.
的解集是_______________________.
查看答案和解析>>
科目:高中数学 来源:2016届福建省晋江市高一年下学期期中考试数学试卷(解析版) 题型:选择题
点 在直线
在直线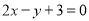 的右下方,则( )
的右下方,则( )
A.2a-b+3<0 B.2a-b+3>0 C.2a-b+3=0 D.以上都不成立
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期期末考试数学试卷(解析版) 题型:解答题
已知数列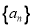 的前
的前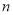 项和为
项和为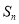 ,且
,且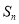 =
= ,数列
,数列 中,
中, ,点
,点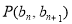 在直线
在直线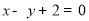 上.
上.
(1)求数列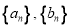 的通项
的通项 和
和 ;
;
(2) 设 ,求数列
,求数列 的前n项和
的前n项和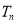 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com