
 )n展开式的各项依次记为a1(x),a2(x),a3(x)…an(x),an+1(x).设F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x).
)n展开式的各项依次记为a1(x),a2(x),a3(x)…an(x),an+1(x).设F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x). •
• ,k=1、2、3,…n+1,
,k=1、2、3,…n+1, =1,
=1, •
• =
= ,
,
 =
= .
. =1+
=1+ ,解得 n=8.
,解得 n=8. +2
+2 •(
•( )+3
)+3 •
•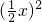 +(n+1)
+(n+1) •
•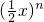 ,
, +2
+2 +3
+3 +…+(n+1)
+…+(n+1) .
. +2
+2 +3
+3 +…+(n+1)
+…+(n+1) ,则有Sn=(n+1)
,则有Sn=(n+1) +n
+n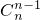 +…+3
+…+3 +2
+2 +
+ .
. =
= 可得 2Sn=(n+2)[
可得 2Sn=(n+2)[ +
+ +
+ +…+
+…+ ]=(n+2)•2n-1,
]=(n+2)•2n-1, •
• ,求得a1(x),a2(x),a3(x)的系数,根据前三项的系数成等差数列求得n的值.
,求得a1(x),a2(x),a3(x)的系数,根据前三项的系数成等差数列求得n的值. +2
+2 +3
+3 +…+(n+1)
+…+(n+1) ,设Sn=
,设Sn= +2
+2 +3
+3 +…+(n+1)
+…+(n+1) ,利用二项式系数的性质求得Sn=(n+2)•2n-2.再利用导数可得F(x)在[0,2]上是增函数可得对任意x1,x2∈[0,2],恒有|F(x1)-F(x2)|≤F(2)-F(0)=2n-1(n+2)-1.
,利用二项式系数的性质求得Sn=(n+2)•2n-2.再利用导数可得F(x)在[0,2]上是增函数可得对任意x1,x2∈[0,2],恒有|F(x1)-F(x2)|≤F(2)-F(0)=2n-1(n+2)-1.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省徐州市诚贤中学高三(上)第二次质量检测数学试卷(解析版) 题型:解答题
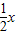 )n展开式的各项依次记为a1(x),a2(x),a3(x)…an(x),an+1(x).设F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x).
)n展开式的各项依次记为a1(x),a2(x),a3(x)…an(x),an+1(x).设F(x)=a1(x)+2a2(x)+2a2(x)+3a3(x)…+nan(x)+(n+1)an+1(x).查看答案和解析>>
科目:高中数学 来源:2011年高三数学精品复习21:排列组合及二项式定理(解析版) 题型:解答题
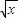 )n的展开式中第9项、第10项、第11项的二项式系数成等差数列,则n= .
)n的展开式中第9项、第10项、第11项的二项式系数成等差数列,则n= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com