
分析 (1)利用三角恒等变换化简函数的解析式,可得f(-$\frac{11π}{12}$)的值.
(2)由条件利用正弦函数的定义域和值域,求得g(x)的最大值和最小值.
解答 解:(1)∵$f(x)=\frac{{{{(1+cos2x)}^2}-2cos2x-1}}{{sin(\frac{π}{4}+x)cos(\frac{π}{4}+x)}}=\frac{{{{cos}^2}2x}}{{\frac{1}{2}sin(\frac{π}{2}+2x)}}=\frac{{2{{cos}^2}2x}}{cos2x}=2cos2x$,
∴$f(-\frac{11π}{12})=2cos(-\frac{11π}{12})=2cos\frac{π}{6}=\sqrt{3}$.
(2)$g(x)=cos2x+sin2x=\sqrt{2}sin(2x+\frac{π}{4})$,
∵$x∈[0,\frac{π}{4})$,
∴$2x+\frac{π}{4}∈[\frac{π}{4},\frac{3π}{4})$,
∴当$x=\frac{π}{8}$时,g(x)有最大值$\sqrt{2}$;当x=0时,g(x)有最小值1.
点评 本题主要考查三角恒等变换,正弦函数的定义域和值域,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{27}{25}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
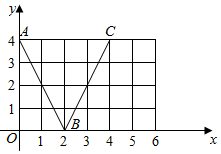 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4),则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4),则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | $[\frac{{\sqrt{2}}}{2},+∞)$ | C. | $[{\frac{{\sqrt{2}}}{4},+∞})$ | D. | $[\sqrt{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 102 | B. | $\frac{865}{8}$ | C. | $\frac{817}{8}$ | D. | 108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com