
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源:不详 题型:解答题
 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙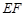 隔开,使得
隔开,使得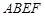 为矩形,
为矩形,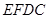 为正方形,设
为正方形,设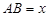 米,已知围墙(包括
米,已知围墙(包括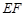 )的修建费用均为800元每米,设围墙(包括
)的修建费用均为800元每米,设围墙(包括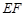 )的修建总费用为
)的修建总费用为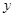 元。
元。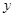 关于
关于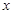 的函数解析式;
的函数解析式;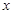 为何值时,设围墙(包括
为何值时,设围墙(包括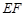 )的的修建总费用
)的的修建总费用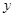 最小?并求出
最小?并求出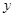 的最小值。
的最小值。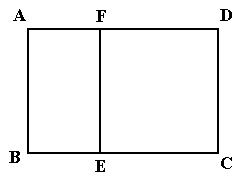
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
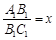 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;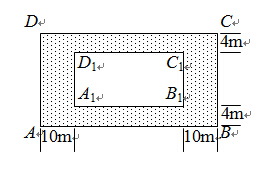
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.?p:?x∈Q,x∉Z | B.?p:?x∉Q,x∈Z |
| C.?p:?x∈Q,x∈Z | D.?p:?x∈Q,x∉Z |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
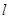 与曲线
与曲线 满足下列两个条件:
满足下列两个条件: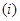 直线
直线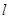 在点
在点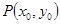 处与曲线
处与曲线 相切;
相切;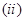 曲线
曲线 在
在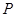 附近位于直线
附近位于直线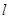 的两侧,则称直线
的两侧,则称直线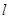 在点
在点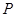 处“切过”曲线
处“切过”曲线 .
.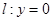 在点
在点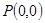 处“切过”曲线
处“切过”曲线 :
: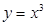
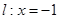 在点
在点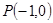 处“切过”曲线
处“切过”曲线 :
: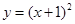
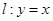 在点
在点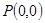 处“切过”曲线
处“切过”曲线 :
: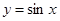
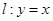 在点
在点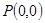 处“切过”曲线
处“切过”曲线 :
: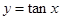
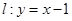 在点
在点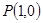 处“切过”曲线
处“切过”曲线 :
: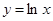
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com