
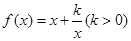 ,
,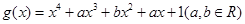 ,(1)若
,(1)若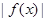 的最小值为2,求
的最小值为2,求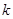 值;(2)设函数
值;(2)设函数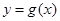 有零点,求
有零点,求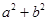 的最小值.
的最小值.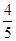 .
.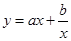 (a>0,b>0)的性质:当
(a>0,b>0)的性质:当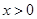 时,在x=
时,在x=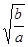 时,取最小值
时,取最小值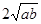 完成求值;(2)本小题等价于方程
完成求值;(2)本小题等价于方程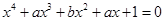 有实根时求
有实根时求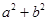 的最小值问题,令
的最小值问题,令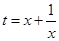 ,问题可化为方程
,问题可化为方程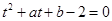 (
(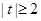 )有实根问题.
)有实根问题.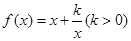 为对勾函数,而
为对勾函数,而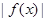 为偶函数,所以只需把问题转化为考虑
为偶函数,所以只需把问题转化为考虑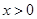 时,
时,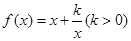 有最小值为2,求
有最小值为2,求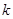 值问题,令
值问题,令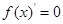 ,可得
,可得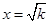 ,代入
,代入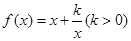 中,有
中,有 ,得
,得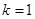 .
.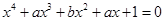 有实根,x=0显然不是根.令
有实根,x=0显然不是根.令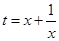 , x为实数,则
, x为实数,则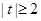 ,同时有:
,同时有: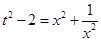 ,方程两边同时除以
,方程两边同时除以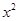 ,得:
,得: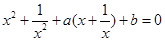 ,即
,即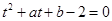 ,此方程有根
,此方程有根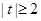 ,令
,令 ,有根则
,有根则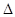 =
=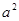 -4(b-2)
-4(b-2) 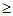 0,若根都在(-2,2),则有
0,若根都在(-2,2),则有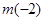 =2-2a+b>0,
=2-2a+b>0, 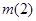 =2+2a+b>0, 即
=2+2a+b>0, 即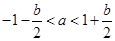 , 也可表为
, 也可表为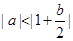 ,故
,故 有
有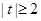 的根的范围是:
的根的范围是: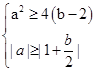 , 即
, 即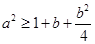 ,故
,故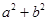
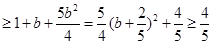 ,当b=
,当b=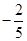 时,a=
时,a=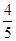 时,
时, 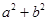 取得最小值
取得最小值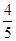 .
.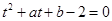 ,则
,则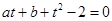 ,从而,
,从而,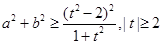 令
令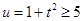 ,从而
,从而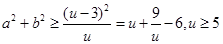 ,从而
,从而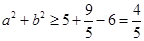 .当且仅当
.当且仅当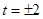 取等号.故
取等号.故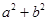 的最小值为
的最小值为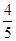 .
.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源:不详 题型:单选题
| A.任意平行四边形的两条对角线不相等或者不相互平分 |
| B.不是平行四边形的四边形两条对角线不相等或者不相互平分 |
| C.存在一个平行四边形,它的两条对角线不相等且不相互平分 |
| D.存在一个平行四边形,它的两条对角线不相等或者不相互平分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com