练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设在三角形ABC中，角A，B，C所对的边分别是a，b，c且满足2a＋2c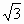＝(＋1)·b

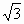    (Ⅰ)求证：2＝(＋1)；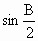

    (Ⅱ)(文)若A＋C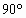＝，试求角C的值．

    (理)若A＝2C，试求角B的值．

    答案：
    解析：

    		 　　解：(Ⅰ)由2a＋2c＝( ＋1)b得2(sinA＋sinC)＝( ＋1)sinB

    　　解：(Ⅰ)由2a＋2c＝(＋1)b得2(sinA＋sinC)＝(＋1)sinB

    　　2·2·＝(＋1)(2)

    　　∵＝＝≠0

    　　即2＝(＋1)(*)

    　　(Ⅱ)(文)若A＋C＝则＝　　＝－C

    　　(*)式可以化为2＝(＋1)

    　　即sinC＋cosC＝

    　　推得sin2C＝且＜2C＜故C＝或

    　　(Ⅱ)(理)依条件A＝2C得B＝－(A＋C)＝－3C

    　　(*)式可以化为2＝(＋1)C

    　　∵≠0，2·＝(＋1)··C

    　　故sinC＝(＋1)·sinC(2cosC－1)

    　　∵sinC≠0　　∴2cosC－1＝＝－1

    　　则：cosC＝且＜C＜

    　　∴C＝，A＝，推得B＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：走向清华北大同步导读·高二数学(上) 题型：044

    在三角形ABC中，顶点A(－，)，并且直线y＝0与直线y＝x平分三角形ABC的内角．求直线BC的方程．

    查看答案和解析>>

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：047

    解答题

    已知a，b，c为三角形三边，x，y，z为不全为零的实数，且x＋y＋z＝0，求证：a2yz＋b3xz＋c2xy＜0．

    查看答案和解析>>

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：047

    已知a，b为不相等的正数，且a3－b3＝a2－b2．

    求证：1＜a＋b＜．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    设向量a＝(cos，cos)，b＝(cos，cos)，u＝a＋tb(t∈R)．

    (1)求a·b；

    (2)求u的模的最小值．

    查看答案和解析>>

    同步练习册答案