Question

设l₁，l₂，l₃为空间中三条互相平行且两两间的距离分别为4，5，6的直线．给出下列三个结论：
①?A_i∈l_i（i=1，2，3），使得△A₁A₂A₃是直角三角形；
②①?A_i∈l_i（i=1，2，3），使得△A₁A₂A₃是等边三角形；
③三条直线上存在四点A_i（i=1，2，3，4），使得四面体A₁A₂A₃A₄为在一个顶点处的三条棱两两互相垂直的四面体．
其中，所有正确结论的序号是（ ）
A．①
B．①②
C．①③
D．②③

Answer 1

【答案】分析：本题利用画图结合运动变化的思想进行分析．我们不妨先将 A、B、C 按如图所示放置，容易看出此时 BC＜AB=AC．
现在，我们将 A 和 B 往上移，并且总保持 AB=AC（这是可以做到的，只要 A、B 的速度满足一定关系），而当A、B 移得很高很高时，就得到①和②都是正确的．至于③，结合条件利用反证法的思想方法进行说明即可．
解答：解：我们不妨先将 A、B、C 按如图所示放置．

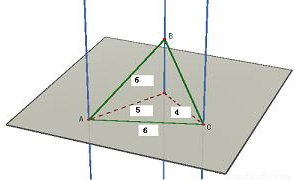
容易看出此时 BC＜AB=AC．
现在，我们将 A 和 B 往上移，并且总保持 AB=AC（这是可以做到的，只要 A、B 的速度满足一定关系），而当A、B 移得很高很高时，不难想象△ABC 将会变得很扁，也就是会变成顶角 A“非常钝”的一个等腰钝角三角形．于是，在移动过程中，总有一刻，使△ABC 成为等边三角形，亦总有另一刻，使△ABC 成为直角三角形（而且还是等腰的）．
这样，就得到①和②都是正确的．
至于③，如图所示．

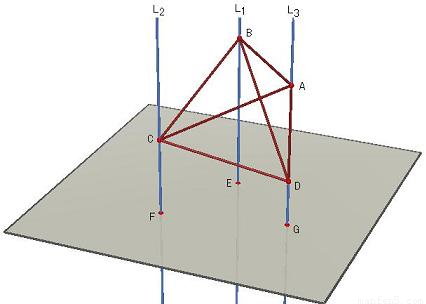
为方便书写，称三条两两垂直的棱所共的顶点为?．
假设 A 是?，那么由 AD⊥AB，AD⊥AC 知 L₃⊥△ABC，从而△ABC 三边的长就是三条直线的距离 4、5、6，这就与 AB⊥AC 矛盾．同理可知 D 是?时也矛盾；
假设 C 是?，那么由 BC⊥CA，BC⊥CD 知 BC⊥△CAD，而 l₁∥△CAD，故 BC⊥l₁，从而 BC 为 l₁与 l₂ 的距离，于是 EF∥BC，EF=BC，这样就得到 EF⊥FG，矛盾．同理可知 B 是?时也矛盾．
综上，不存在四点A_i（i=1，2，3，4），使得四面体A₁A₂A₃A₄为在一个顶点处的三条棱两两互相垂直的四面体．
故选B．
点评：本小题主要考查命题的真假判断与应用，考查空间想象能力、化归与转化思想．属于难题．