
有一个容量为100的样本,数据的分组及各组的频数如下: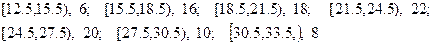
(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图。
(1)样本的频率分布表;
科目:高中数学
来源:
题型:解答题
甲,乙两机床同时加工直径为100cm的零件,为检验质量,各从中抽取6件测量的数据为:甲:99,100,98,100,100,103 乙:99,100, 102, 99,100 ,100
科目:高中数学
来源:
题型:解答题
(12分) 假设关于某设备的使用年限
科目:高中数学
来源:
题型:解答题
(本题满分12分)为了让生了解环保知识,增强环保意识,某中举行了一次“环保知识竞赛”,共有900名生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
科目:高中数学
来源:
题型:解答题
某研究机构为研究人的脚的大小与身高之间的关系,随机抽测了
科目:高中数学
来源:
题型:解答题
(本小题满分10分)某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成
科目:高中数学
来源:
题型:解答题
(本小题共13分)
科目:高中数学
来源:
题型:解答题
(本题满分14分)
科目:高中数学
来源:
题型:解答题
(本小题满分12分)第16届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区分组 频数 频率 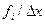
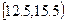
6 0.06 0.02 
16 0.16 0.053 
18 0.18 0.06 
22 0.22 0.073 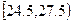
20 0.20 0.067 
10 解析



西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
(1)分别计算两组数据的平均数及方差
(2)根据计算结果判断哪台机床加工零件的质量更稳定. 和所支出的维修费用
和所支出的维修费用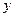 (万元)有如下的统计数据,由资料显示
(万元)有如下的统计数据,由资料显示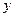 对
对 呈线性相关关系.
呈线性相关关系. x 3 4 5 6 y 2.5 3 4 4.5
(2)试根据(1)求出的线性回归方程,预测使用年限为10年时, 维修费用是多少?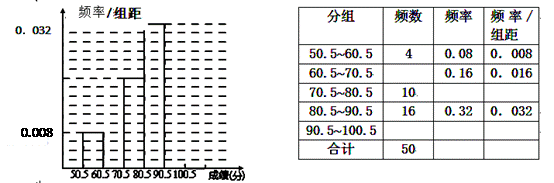
(1)若用系统抽样的方法抽取50个样本,现将所有生随机地编号为
000,001,002,…,899,试写出第二组第一位生的编号 ;
(2)填充频率分布表的空格(将答案直接填在表格内)和补全频率分布直方图
(3)所抽取的这些数据的中位数可能在直方图的哪一组?
(4)若成绩在75.5~85.5分的生为二等奖,估计获二等奖的生为多少人?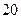 人,得到如下数据:
人,得到如下数据:序号
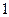
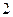
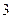
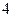
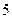
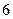
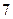

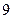
身高 
脚长  (码)
(码)
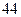
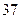
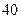

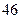

序号
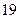
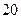
身高 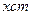
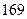
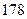
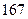
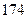
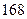

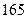
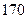
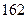
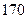
脚长  (码)
(码)
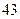
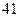
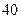
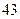
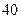
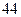
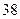
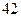

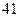
(1)若“身高大于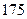 厘米”的为“高个”,“身高小于等于
厘米”的为“高个”,“身高小于等于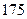 厘米”的为“非高个”;“脚长大于
厘米”的为“非高个”;“脚长大于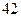 码”的为“大脚”,“脚长小于等于
码”的为“大脚”,“脚长小于等于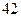 码”的为“非大脚”.
码”的为“非大脚”.
请根据上表数据完成下面的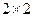 列联表:
列联表:
高 个
非高个
合 计
大 脚
非大脚
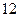
合 计
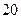
(2)根据题(1)中表格的数据,检验人的脚的大小与身高之间是否有关系,若有关系指出判断有关系的把握性有多大?
六组[40, 50),[50,60)...[90,100]后画出如下部分频率分布直方图.观察图形的信息,
50),[50,60)...[90,100]后画出如下部分频率分布直方图.观察图形的信息,
回 答下列问题:
答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,
并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(6 0分及
0分及
以上为及格)和平均分.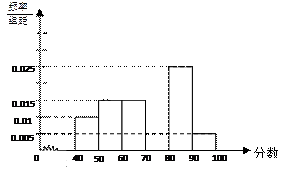
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为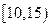 ,
, ,
, ,
, ,
,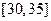 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
人不在同一组的概率是多少?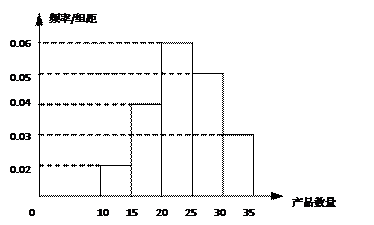
某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水
化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳
水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中
至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,
并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
喜爱运动
不喜爱运动
总计
男
10
16
女
6
14
总计
30
(3)从女志原者中抽取2人参加接待工作,若其中喜爱运动的人数为 ,求
,求 的分布列和均值。
的分布列和均值。
参考公式: ,其中
,其中
参考数据:
0.40
0.25
0.10
0.010

0.708
1.323
2.706
6.635
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号