
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以![]() 为底面)
为底面)
被一平面所截得到的几何体,截面为ABC.
已知![]() .
.
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)证明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此几何体的体积.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以![]() 为底面)
为底面)
被一平面所截得到的几何体,截面为ABC.
已知![]() .
.
(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)证明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此几何体的体积.
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下期中理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
右图为一简单组合体,其底面ABCD为正方形,
 平面
平面 ,
, ,且
,且 =2 .
=2 .
(1)求证: 平面
平面 ;
;
(2)求四棱锥B-CEPD的体积.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期第一次调研考试数学试卷(实验班) 题型:解答题
(本小题14分)某企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如左图, B产品的利润与投资的算术平方根成正比,其关系如右图 (注:利润与投资单位:万元).
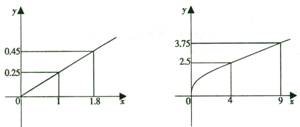
(1)分别将A、B两种产品的利润表示为投资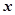 (万元)的函数关系式;
(万元)的函数关系式;
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题14分)执行右图中程序,回答下面问题。
|
(2)画出该程序的程序框图。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com