Question

等比数列{a_n}中，a_n＞0，a₁+a₂+a₃=7，a₅-a₂=14，n∈N^*．
（1）求a_n；
（2）求数列{log₂a_n}的前10项和．

Answer 1

解：（1）设公比为q，显然q＞0且q≠1
由a₁+a₂+a₃=7得a₁（1+q+q²）①
由a₅-a₂=14得a₁q（q³-1）=14②
②÷①得q（q-1）=2得q=2或q=-1（舍）
∴a₁=1，故a_n=2^n-1
（2）∵a_n=2^n-1，∴log₂a_n=n-1，
∴数列{log₂a_n}是以0为首项，1为公差的等差数列，
∴
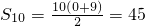
分析：（1）设出等比数列的公比为q，代入a₁+a₂+a₃=7，a₅-a₂=14，，得到关于首项与公比的二元一次方程组，求出方程组的解即可得到首项和公比的值，根据首项和公比写出相应的通项公式即可；
（2）把（1）求得的结果代入log₂a_n中，得到log₂a_n=n-1，可知数列{log₂a_n}是一个等差数列，利用等差数列前n相和公式即可求得结果．
点评：此题考查学生灵活运用等比数列的通项公式及等差数列前n项和的公式化简求值，其中根据对数的运算法则求得数列{log₂a_n}是一个等差数列，是解题的关键，属道基础题．