
科目:高中数学 来源:2016届辽宁省抚顺市高三12月月考理科数学试卷(解析版) 题型:解答题
设数列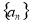 的前
的前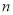 项和
项和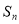 满足:
满足: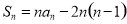 ,等比数列
,等比数列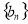 的前
的前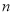 项和为
项和为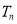 ,公比为
,公比为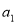 ,且
,且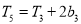 .
.
(1)求数列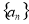 的通项公式;
的通项公式;
(2)设数列 的前
的前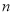 项和为
项和为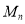 ,求证:
,求证: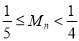 .
.
查看答案和解析>>
科目:高中数学 来源:2016届浙江省绍兴市高三上学期期中文科数学试卷(解析版) 题型:选择题
以 为底边的等腰三角形
为底边的等腰三角形 中,
中, 边上的中线长为
边上的中线长为 ,当
,当 面积最大时,腰
面积最大时,腰 长为( )
长为( )
A.  B.
B.  C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届辽宁省沈阳市高三上学期期中文科数学试卷(解析版) 题型:解答题
“水资源与永恒发展”是2015年联合国世界水资源日主题.近年来,某企业每年需要向自来水厂缴纳水费约4万元,为了缓解供水压力,决定安装一个可使用4年的自动污水净化设备,安装这种净水设备的成本费(单位:万元)与管线、主体装置的占地面积(单位:平方米)成正比,比例系数约为0.2.为了保证正常用水,安装后采用净水装置净水和自来水厂供水互补的用水模式.假设在此模式下,安装后该企业每年向自来水厂缴纳的水费 C(单位:万元)与安装的这种净水设备的占地面积x(单位:平方米)之间的函数关系是 (x≥0,k为常数).记y为该企业安装这种净水设备的费用与该企业4年共将消耗的水费之和.
(x≥0,k为常数).记y为该企业安装这种净水设备的费用与该企业4年共将消耗的水费之和.
(1) 试解释  的实际意义,请建立y关于x的函数关系式并化简;
的实际意义,请建立y关于x的函数关系式并化简;
(2) 当x为多少平方米时,y取得最小值?最小值是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com