已知 3cos2α+2sin2α=-1.
求:(1)tanα的值;
(2)3cos2α+4sin2α的值.
【答案】
分析:(1)将已知的等式右边的-1移项到左边,并把1化为sin
2α+cos
2α,并利用二倍角的正弦函数公式化简,然后利用完全平方公式整理后,开方可得出2cosα=-sinα,等式左右两边同时除以cosα,利用同角三角函数间的基本关系弦化切后,即可求出tanα的值;
(2)把所求式子分别利用二倍角的正弦、余弦函数公式化简,再利用同角三角函数间的基本关系把“1”化为sin
2α+cos
2α,同时将分母“1”化为sin
2α+cos
2α,整理后分子分母同时除以cos
2α,利用同角三角函数间的基本关系弦化切后,将tanα的值代入即可求出值.
解答:解:(1)∵3cos
2α+2sin2α=-1,即3cos
2α+4sinαcosα+1=0,
变形为4cos
2α+4sinαcosα+sin
2α=0,即(2cosα+sinα)
2=0,
∴2cosα=-sinα,
∴tanα=-2;…(5分)
(2)3cos2α+4sin2α=3(2cos
2α-1)+8sinαcosα=3(cos
2α-sin
2α)+8sinαcosα
=

=
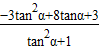
=-5.…(10分)
点评:此题考查了同角三角函数间的基本关系,以及二倍角的正弦、余弦函数公式,熟练掌握基本关系及公式是解本题的关键.

 =
=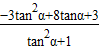 =-5.…(10分)
=-5.…(10分)
