
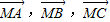 的起点与终点M、A、B、C互不重合且无三点共线,且满足下列关系(O为空间任一点),则能使向量
的起点与终点M、A、B、C互不重合且无三点共线,且满足下列关系(O为空间任一点),则能使向量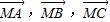 成为空间一组基底的关系是( )
成为空间一组基底的关系是( )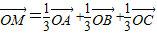
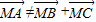
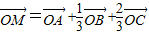
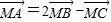
科目:高中数学 来源: 题型:
| MA |
| MB |
| MC |
| MA |
| MB |
| MC |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
①若向量a、b的夹角为θ,则cosθ=![]() ;
;
②(a+b)·c=a·c+b·c;
③若向量![]() 的起点为A(-2,4),终点为B(2,1),则
的起点为A(-2,4),终点为B(2,1),则![]() 与x轴正方向所夹角的余弦值是
与x轴正方向所夹角的余弦值是![]() ;
;
④若向量a=(m,4),且|a|=![]() ,则m=
,则m=![]() .其中不正确命题的序号有____________.
.其中不正确命题的序号有____________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| MA |
| MB |
| MC |
| MA |
| MB |
| MC |
A.
| B.
| ||||||||||||||||||||
C.
| D.
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com