
分析 可以设楼高设计为n层时,平均每平方米建筑面积的成本费为y元,每平方米建筑面积的成本费有两部分组成,一部分是土地使用权取得费,一部分是材料工程费,将两部分的费用相加再除以层数n,即可求出平均每平方米建筑面积的成本费,最后利用基本不等式进行求解即可.
解答 解:设楼高设计为n层时,平均每平方米建筑面积的成本费为y元.(n∈N*)
依题意得:y=$\frac{2000+[400+(400+40)+(400+40×2)+…+(400+40×(n-1))]}{n}$
=$\frac{2000+400n+40[1+2+3+…+(n-1)]}{n}$=$\frac{2000+380n+20{n}^{2}}{n}$
=20($\frac{100}{n}$+n+19)≥20(2×10+19)=780(当且仅当n=10时,等号成立)
故答案为:10.
点评 此题是关于建造楼房的问题,在生活中,安居工程确实是老百姓比较关心的问题之一,解决此题的关键要读懂题意,本题是等差数列的模型,列出合适的式子,进而求解.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
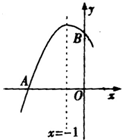 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com