
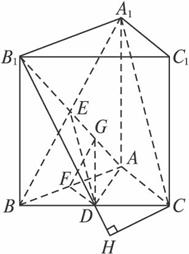
(1)求证:A1C∥平面AB1D;
(2)求二面角BAB1D的大小;
(3)求点C到平面AB1D的距离.
(文)如图,正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB.
(1)求证:AD⊥B1D;
(2)求证:A1C∥平面AB1D;
(3)求二面角BAB1D的大小.
答案:(理)解法一:
(1)证明:连接A1B,设A1B∩AB1=E,连接DE.

∵ABC—A1B1C1是正三棱柱,且AA1=AB,∴四边形A1ABB1是正方形.∴E是A1B的中点.又D是BC的中点,∴DE∥A1C.
∵DE![]() 平面AB1D,A1C
平面AB1D,A1C![]() 平面AB1D,∴A1C∥平面AB1D.
平面AB1D,∴A1C∥平面AB1D.
(2)解:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG.
∵平面A1ABB1⊥平面ABC,∴DF⊥平面A1ABB1.∴FG是DG在平面A1ABB1上的射影.∵FG⊥AB1,∴DG⊥AB1.∴∠FGD是二面角BAB1D的平面角.
设A1A=AB=1,在正△ABC中,DF=![]() ,
,
在△ABE中,FG=![]() BE=
BE=![]() ,
,
在Rt△DFG中,tan∠FGD=![]() ,所以,二面角BAB1D的大小为arctan
,所以,二面角BAB1D的大小为arctan![]() .
.
(3)解:∵平面B1BCC1⊥平面ABC,且AD⊥BC,∴AD⊥平面B1BCC1.又AD![]() 平面AB1D,∴平面B1BCC1⊥平面AB1D.在平面B1BCC1内作CH⊥B1D交B1D的延长线于点H,则CH的长度就是点C到平面AB1D的距离.
平面AB1D,∴平面B1BCC1⊥平面AB1D.在平面B1BCC1内作CH⊥B1D交B1D的延长线于点H,则CH的长度就是点C到平面AB1D的距离.
由△CDH∽△B1DB,得CH=![]() ,即点C到平面AB1D的距离是
,即点C到平面AB1D的距离是![]() .
.
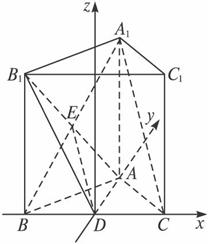
解法二:建立空间直角坐标系D—xyz,如图.

(1)证明:连接A1B,设A1B∩AB1=E,连接DE.设A1A=AB=1,
则D(0,0,0),A1(0,![]() ,1),E(-
,1),E(-![]() ,
,![]() ,
,![]() ),C(
),C(![]() ,0,0).∴
,0,0).∴![]() =(
=(![]() ,-
,-![]() ,-1),
,-1),![]() =(-
=(-![]() ,
,![]() ,
,![]() ).
).
∴![]() =-2
=-2![]() .∴A1C∥DE.
.∴A1C∥DE.
∵DE![]() 平面AB1D,A1C
平面AB1D,A1C![]() 平面AB1D,∴A1C∥平面AB1D.
平面AB1D,∴A1C∥平面AB1D.
(2)解:∵A(0,![]() ,0),B1(-
,0),B1(-![]() ,0,1),∴
,0,1),∴![]() =(0,-
=(0,-![]() ,0),
,0),![]() =(
=(![]() ,0,-1).设n1=(p,q,r)是平面AB1D的法向量,则n1·
,0,-1).设n1=(p,q,r)是平面AB1D的法向量,则n1·![]() =0,且n1·
=0,且n1·![]() =0,故-
=0,故-![]() q=0,
q=0,![]() p-r=0.取r=1,得n1=(2,0,1);
p-r=0.取r=1,得n1=(2,0,1);
同理,可求得平面AB1B的法向量是n2=(![]() ,-1,0).
,-1,0).
设二面角BAB1D的大小为θ,∵cosθ=![]() ,
,
∴二面角BAB1D的大小为arccos![]() .
.
(3)解:由(2)得平面AB1D的法向量为n1=(2,0,1),
取其单位法向量n=(![]() ,0,
,0,![]() ),又
),又![]() =(
=(![]() ,0,0),
,0,0),
∴点C到平面AB1D的距离d=|![]() ·n|=
·n|=![]() .
.
(文)解法一:(1)证明:

∵ABC—A1B1C1是正三棱柱,∴BB1⊥平面ABC.∴BD是B1D在平面ABC上的射影.在正△ABC中,∵D是BC的中点,∴AD⊥BD.根据三垂线定理得AD⊥B1D.
(2)证明:连接A1B,设A1B∩AB1=E,连接DE.∵AA1=AB,∴四边形A1ABB1是正方形.∴E是A1B的中点.又D是BC的中点,∴DE∥A1C.
∵DE![]() 平面AB1D,A1C
平面AB1D,A1C![]() 平面AB1D,∴A1C∥平面AB1D.
平面AB1D,∴A1C∥平面AB1D.
(3)解:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG.∵平面A1ABB1⊥平面ABC,∴DF⊥平面A1ABB1.∴FG是DG在平面A1ABB1上的射影.∵FG⊥AB1,∴DG⊥AB1.∴∠FGD是二面角BAB1D的平面角.
设A1A=AB=1,在正△ABC中,DF=![]() ,在△ABE中,FG=
,在△ABE中,FG=![]() BE=
BE=![]() ,
,
在Rt△DFG中,tan∠FGD=![]() =
=![]() ,所以二面角BAB1D的大小为arctan
,所以二面角BAB1D的大小为arctan![]() .
.
解法二:建立空间直角坐标系D—xyz,如图.

则D(0,0,0),A(0,![]() ,0),B1(-
,0),B1(-![]() ,0,1).
,0,1).
(1)证明:∵![]() =(0,-
=(0,-![]() ,0),
,0),![]() =(
=(![]() ,0,-1),∴
,0,-1),∴![]() =0.∴
=0.∴![]() ⊥
⊥![]() ,即AD⊥B1D.
,即AD⊥B1D.
(2)证明:连接A1B,设A1B∩AB1=E,连接DE.∵A1(0,![]() ,1),E(-
,1),E(-![]() ,
,![]() ,
,![]() ),C(
),C(![]() ,0,0),
,0,0),
∴![]() =(
=(![]() ,-
,-![]() ,-1),
,-1),![]() =(-
=(-![]() ,
,![]() ,
,![]() ).∴
).∴![]() =-2
=-2![]() .∴A1C∥DE.
.∴A1C∥DE.
∵DE![]() 平面AB1D,A1C
平面AB1D,A1C![]() 平面AB1D,∴A1C∥平面AB1D.
平面AB1D,∴A1C∥平面AB1D.
(3)解:设n1=(p,q,r)是平面AB1D的法向量,则n1·![]() =0,且n1·
=0,且n1·![]() =0,故-
=0,故-![]() q=0,
q=0,![]() p-r=0.取r=1,得n1=(2,0,1);同理,可求得平面AB1B的法向量是n2=(
p-r=0.取r=1,得n1=(2,0,1);同理,可求得平面AB1B的法向量是n2=(![]() ,-1,0).
,-1,0).
设二面角BAB1D的大小为θ,∵cosθ=![]() ,
,
∴二面角BAB1D的大小为arccos![]() .
.


科目:高中数学 来源: 题型:
(07年西城区抽样测试理)(14分) 如图,正三棱柱ABC―A1B1C1中,D是BC的中点,AA1=AB=1.
(I)求证:A1C//平面AB1D;
(II)求二面角B―AB1―D的大小;
(III)求点c到平面AB1D的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
(03年北京卷理)(12分)
如图,正四棱柱ABCD―A1B1C1D1中,底面边长为![]() ,侧棱长为4.E,F分别为棱AB,BC的中点,
,侧棱长为4.E,F分别为棱AB,BC的中点,
EF∩BD=G.
(Ⅰ)求证:平面B1EF⊥平面BDD1B1;
(Ⅱ)求点D1到平面B1EF的距离d;
(Ⅲ)求三棱锥B1―EFD1的体积V.

查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二上学期数学单元测试4 题型:解答题
(理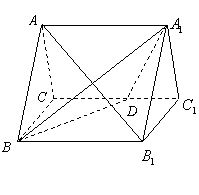 )如图,正三棱柱
)如图,正三棱柱 的所有棱长都为
的所有棱长都为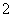 ,
, 为
为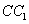 中点.
中点.
(Ⅰ)求证: 平面
平面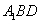 ;
;
(Ⅱ)求二面角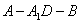 的大小;
的大小;
(Ⅲ)求点 到平面
到平面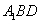 的距离.
的距离.
(文)设函数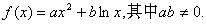
证明:当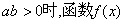 没有极值点;当
没有极值点;当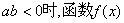 有且只有一个极值点,并求出极值
有且只有一个极值点,并求出极值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com