
分析 (Ⅰ)将两向量的模用坐标表示出来,探究发现点M到两个定点之间的距离和为6,符合椭圆的定义.用定义法写出其标准方程即可.
(Ⅱ)先把直线方程和椭圆方程联立,求出关于点A和点B的坐标的方程①,在利用OAPB为矩形转化为OA⊥OB既为$\overrightarrow{OA}•\overrightarrow{OB}$=0.把①式代入就可求直线AB的方程.
解答 解:(I)∵$\overrightarrow{a}$=(x+1)i+yj,$\overrightarrow{b}$=(x-1)i+yj
又|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=4,∵$\sqrt{(x+1)^{2}+{y}^{2}}+\sqrt{(x-1)^{2}+{y}^{2}}=6$.
∴点M(x,y)的轨迹C是以(-1,0)、(1,0)为焦点,长轴长为6的椭圆,
故椭圆方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$.
(Ⅱ)由条件(2)可知OAB不共线,故直线AB的斜率存在,
设AB方程为y=kx+1,A(x1,y1),B(x2,y2)
由$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1}\end{array}\right.$⇒(9k2+8)x2+18kx-63=0,
${x}_{1}+{x}_{2}=\frac{-18k}{9{k}^{2}+8}$,${x}_{1}{x}_{2}=\frac{-63}{9{k}^{2}+8}$
y1•y2=(kx1+1)•(kx2+1)=k2x1•x2+k(x1+x2)+1=$\frac{-72{k}^{2}+8}{9{k}^{2}+8}$
∵OAPB为矩形,∴OA⊥OB⇒$\overrightarrow{OA}•\overrightarrow{OB}$=0.
∴x1•x2+y1•y2=0得72k2=-55,方程无解,
∴不存在直线l,使得四边形OAPB是矩形.
点评 本题综合考查了直线与椭圆的位置关系以及向量垂直问题.在研究直线和圆锥曲线问题时,通常把直线方程和圆锥曲线方程联立,找到关于二者交点坐标的方程,再代入已知条件解题.属于中档题.


科目:高中数学 来源: 题型:解答题
| 甲班 | 乙班 | 丙班 | |
| 男同学 | A | B | C |
| 女同学 | X | Y | Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥S-ABC中,SA⊥底面ABC,SA=AB=$\frac{1}{2}$AC=a,∠BAC=60°,D是SC上的点.
如图,在三棱锥S-ABC中,SA⊥底面ABC,SA=AB=$\frac{1}{2}$AC=a,∠BAC=60°,D是SC上的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-y<1 | B. | lnx>lny | C. | sin x>sin y | D. | x3>y3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 1008 | C. | 504 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
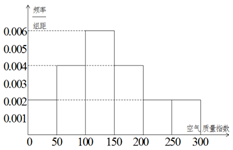 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度 污染 | 4级中度 污染 | 5级重度 污染 | 6级严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com