
【题目】已知命题p:“x∈[1,2],![]() x2-lnx-a≥0”与命题q:“x∈R,x2+2ax-8-6a=0”都是真命题,求实数a的取值范围.
x2-lnx-a≥0”与命题q:“x∈R,x2+2ax-8-6a=0”都是真命题,求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 满足约束条件
满足约束条件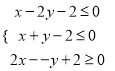 ,若
,若![]() 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数![]() 的值为__________.
的值为__________.
【答案】![]() 或
或![]()
【解析】由题可知若![]() 取得最大值的最优解不唯一则
取得最大值的最优解不唯一则![]() 必平行于可行域的某一边界,如图:
必平行于可行域的某一边界,如图: 要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
要Z最大则直线与y轴的截距最大即可,当a<0时,则平行AC直线即可故a=-2,当a>0时,则直线平行AB即可,故a=1
点睛:线性规划为常考题型,解决此题务必要理解最优解个数为无数个时的条件是什么,然后根据几何关系求解即可
【题型】填空题
【结束】
16
【题目】《数书九章》三斜求积术:“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约一,为实,一为从隅,开平方得积”.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,“术”即方法.以![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别表示三角形的面积,大斜,中斜,小斜;
分别表示三角形的面积,大斜,中斜,小斜; ![]() ,
, ![]() ,
, ![]() 分别为对应的大斜,中斜,小斜上的高;则
分别为对应的大斜,中斜,小斜上的高;则
![]()
![]() .若在
.若在![]() 中
中![]() ,
, ![]() ,
, ![]() ,根据上述公式,可以推出该三角形外接圆的半径为__________.
,根据上述公式,可以推出该三角形外接圆的半径为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是棱长为2的正方形,E为AD的中点,以CE为折痕把△DEC折起,使点D到达点P的位置,且点P的射影O落在线段AC上.
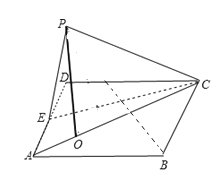
(1)求![]() ;
;
(2)求几何体P﹣ABCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数为![]() (α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ;
;
(1)写出曲线C的普通方程和直线l的参数方程;
(2)设点P(m,0),若直线l与曲线C相交于A,B两点,且|PA|![]() |PB|=1,求实数m的值.
|PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知拋物线C:![]() 经过点
经过点![]() ,其焦点为F,M为抛物线上除了原点外的任一点,过M的直线l与x轴、y轴分别交于A,B两点.
,其焦点为F,M为抛物线上除了原点外的任一点,过M的直线l与x轴、y轴分别交于A,B两点.
![]() Ⅰ
Ⅰ![]() 求抛物线C的方程以及焦点坐标;
求抛物线C的方程以及焦点坐标;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 的面积相等,证明直线l与抛物线C相切.
的面积相等,证明直线l与抛物线C相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的![]() 名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取
名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取![]() 名学生的数学成绩(满分:
名学生的数学成绩(满分:![]() 分),并绘制成如图所示的茎叶图.将成绩低于
分),并绘制成如图所示的茎叶图.将成绩低于![]() 分的称为“不及格”,不低于
分的称为“不及格”,不低于![]() 分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
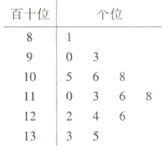
(1)估算此次联考该校高三学生的数学学科的平均成绩.
(2)估算此次联考该校高三学生数学成绩“不及格”和“优秀”的人数各是多少.
(3)在国家扶贫政策的倡导下,该地教育部门提出了教育扶贫活动,要求对此次数学成绩“不及格”的学生分两期进行学业辅导:一期由优秀学生进行一对一帮扶辅导,二期由老师进行集中辅导.根据实践总结,优秀学生进行一对一辅导的转化率为![]() ;老师集中辅导的转化率为
;老师集中辅导的转化率为![]() ,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
注:转化率![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是以
是以![]() 为焦点的抛物线
为焦点的抛物线![]() ,
,![]() 是以直线
是以直线![]() 与
与![]() 的渐近线,以
的渐近线,以![]() 为一个焦点的双曲线.
为一个焦点的双曲线.
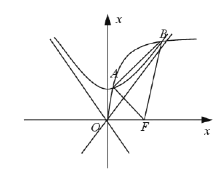
(1)求双曲线![]() 的标准方程;
的标准方程;
(2)若![]() 与
与![]() 在第一象限有两个公共点
在第一象限有两个公共点![]() ,求
,求![]() 的取值范围,并求
的取值范围,并求![]() 的最大值;
的最大值;
(3)是否存在正数![]() ,使得此时
,使得此时![]() 的重心
的重心![]() 恰好在双曲线
恰好在双曲线![]() 的渐近线上?如果存在,求出
的渐近线上?如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车零件加工厂为迎接国庆大促销活动预估国庆七天销售量,该厂工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
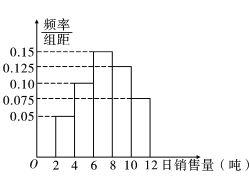
(1)根据频率分布直方图估计该厂的日平均销售量;(每组以中点值为代表)
(2)求未来![]() 天内,连续
天内,连续![]() 天日销售量不低于
天日销售量不低于![]() 吨,另一天日销售量低于
吨,另一天日销售量低于![]() 吨的概率;
吨的概率;
(3)用![]() 表示未来
表示未来![]() 天内日销售量不低于
天内日销售量不低于![]() 吨的天数,求随机变量
吨的天数,求随机变量![]() 的分布列、数学期望与方差.
的分布列、数学期望与方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com