
.设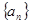 是公比为
是公比为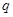 的等比数列,
的等比数列,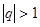 ,令
,令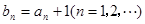 ,若数列
,若数列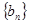 有连续四项在集合
有连续四项在集合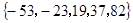 中,则
中,则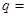 ★ .
★ .
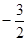
解析考点:等比数列的性质.
分析:根据bn=an+1可知 an=bn-1,依据{bn}有连续四项在{-53,-23,19,37,82}中,则可推知则{an}有连续四项在{-54,-24,18,36,81}中,按绝对值的顺序排列上述数值,可求{an}中连续的四项,求得q
解:{bn}有连续四项在{-53,-23,19,37,82}中且bn=an+1 an=bn-1
则{an}有连续四项在{-54,-24,18,36,81}中
∵{an}是等比数列,等比数列中有负数项则q<0,且负数项为相隔两项
∴等比数列各项的绝对值递增或递减,按绝对值的顺序排列上述数值18,-24,36,-54,81}
相邻两项相除-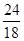 =-
=-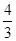 ,-
,- =-
=-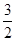 ,-
,- =-
=-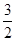 ,
, =-
=-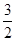
则可得,-24,36,-54,81是{an}中连续的四项,此时q=-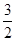


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
设![]() 个不全相等的正数
个不全相等的正数![]() 依次围成一个圆圈.
依次围成一个圆圈.
(Ⅰ)若![]() ,且
,且![]() 是公差为
是公差为![]() 的等差数列,而
的等差数列,而![]() 是公比为
是公比为![]() 的等比数列;数列
的等比数列;数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() ,求通项
,求通项![]() ;
;
(Ⅱ)若每个数![]() 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证:![]() ;
; ![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
设![]() 个不全相等的正数
个不全相等的正数![]() 依次围成一个圆圈。
依次围成一个圆圈。
(Ⅰ)若![]() ,且
,且![]() 是公差为
是公差为![]() 的等差数列,而
的等差数列,而![]() 是公比为
是公比为![]() 的等比数列;数列
的等比数列;数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() ,求通项
,求通项![]() ;
;
(Ⅱ)若每个数![]() 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证:![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() 个不全相等的正数
个不全相等的正数![]() 依次围成一个圆圈。
依次围成一个圆圈。
(Ⅰ)若![]() ,且
,且![]() 是公差为
是公差为![]() 的等差数列,而
的等差数列,而![]() 是公比为
是公比为![]() 的等比数列;数列
的等比数列;数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() ,求通项
,求通项![]() ;
;
(Ⅱ)若每个数![]() 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证:![]() 。
。
查看答案和解析>>
科目:高中数学 来源:2009高考真题汇编3-数列 题型:解答题
(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
设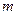 个不全相等的正数
个不全相等的正数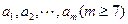 依次围成一个圆圈。
依次围成一个圆圈。
(Ⅰ)若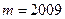 ,且
,且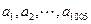 是公差为
是公差为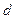 的等差数列,而
的等差数列,而 是公比为
是公比为 的等比数列;数列
的等比数列;数列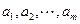 的前
的前 项和
项和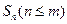 满足:
满足: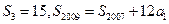 ,求通项
,求通项 ;
;
(Ⅱ)若每个数 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证: 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com