
【题目】如图直三棱柱ABC﹣A1B1C1 中AC=2AA1 , AC⊥BC,D、E 分别为A1C1、AB 的中点.求证: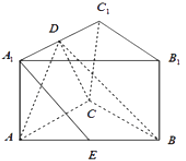
(1)AD⊥平面BCD
(2)A1E∥平面BCD.
【答案】
(1)证明:∵直三棱柱ABC﹣A1B1C1中CC1⊥平面ABC,又BC平面ABC,
∴CC1⊥BC,
又∵AC⊥BC,AC∩CC1=C,AC,CC1平面AA1C1C,
∴BC⊥平面AA1C1C,
而AD平面AA1C1C∴BC⊥AD①
又该直三棱柱中AA1⊥A1C1,CC1⊥A1C1,
由已知AA1= ![]() AC=A1D,则∠A1DA=
AC=A1D,则∠A1DA= ![]() ,
,
同理∠C1DC= ![]() ,则∠ADC=
,则∠ADC= ![]() ,即CD⊥AD,
,即CD⊥AD,
由①BC⊥AD,BC∩CD=C,BC,CD平面BCD,
∴AD⊥平面BCD
(2)证明:取BC中点O,连结DO、OE,∵AE=EB,CO=BO∴OE平行等于 ![]() AC,
AC,
而A1D平行等于 ![]() AC,
AC,
∴A1D平行等于OE∴四边形A1DOE为平行四边形,
∴A1E∥OD,而A1E平面BCD,OD平面BCD,
∴A1E∥平面BCD.
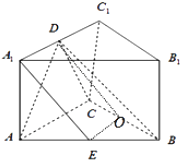
【解析】(1)只需证明BC⊥AD,DC⊥AD,证明 即可AD⊥平面BCD(2)取BC中点O,连结DO、OE可得四边形A1DOE为平行四边形,即A1E∥OD,A1E∥平面BCD.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() ﹣2alnx(a∈R) (Ⅰ)若函数f(x)在x=2时取极值,求实数a的值;
﹣2alnx(a∈R) (Ⅰ)若函数f(x)在x=2时取极值,求实数a的值;
(Ⅱ)若f(x)≥0对任意x∈[1,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
(Ⅰ)请在图中补全频率分布直方图;
(Ⅱ)若Q大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
①若Q大学本次面试中有B、C、D三位考官,规定获得两位考官的认可即面试成功,且面试结果相互独立,已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为 ![]() 、
、 ![]() ,
, ![]() ,求甲同学面试成功的概率;
,求甲同学面试成功的概率;
②若Q大学决定在这6名学生中随机抽取3名学生接受考官B的面试,第3组中有ξ名学生被考官B面试,求ξ的分布列和数学期望.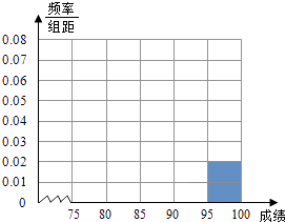
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为双曲线C: ![]() (a>0,b>0)的右焦点,l1 , l2为C的两条渐近线,点A在l1上,且FA⊥l1 , 点B在l2上,且FB∥l1 , 若
(a>0,b>0)的右焦点,l1 , l2为C的两条渐近线,点A在l1上,且FA⊥l1 , 点B在l2上,且FB∥l1 , 若 ![]() ,则双曲线C的离心率为( )
,则双曲线C的离心率为( )
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axlnx+bx(a≠0)在(1,f(1))处的切线与x轴平行,(e=2.71828)
(1)试讨论f(x)在(0,+∞)上的单调性;
(2)①设g(x)=x+ ![]() ,x∈(0,+∞),求g(x)的最小值; ②证明:
,x∈(0,+∞),求g(x)的最小值; ②证明: ![]() ≥1﹣x.
≥1﹣x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若 ![]() 是函数
是函数 ![]() 图象的一条对称轴,当ω取最小正数时( )
图象的一条对称轴,当ω取最小正数时( )
A.f(x)在 ![]() 单调递减
单调递减
B.f(x)在 ![]() 单调递增
单调递增
C.f(x)在 ![]() 单调递减
单调递减
D.f(x)在 ![]() 单调递增
单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如表: 
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则5288用算筹式可表示为 .
,则5288用算筹式可表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com