
| A. | (1,-$\sqrt{3}$) | B. | (-1,$\sqrt{3}$) | C. | ($\sqrt{3}$,-1) | D. | (-$\sqrt{3}$,1) |
分析 由点M的极坐标是(2,$\frac{5π}{3}$)得出ρ=2,θ=$\frac{5π}{3}$,根据x=ρ•cosθ,y=ρ•sinθ,求出点M的直角坐标.
解答 解:∵点M的极坐标是(2,$\frac{5π}{3}$),
∴ρ=2,θ=$\frac{5π}{3}$
∴x=ρ•cosθ=2$•cos\frac{5π}{3}$=1,y=$ρ•sinθ=2•sin\frac{5π}{3}$=-$\sqrt{3}$
∴点M的直角坐标是(1,-$\sqrt{3}$).
故选:A.
点评 本题考查了点的极坐标与直角坐标的转化,要记住基本公式x=ρ•cosθ,y=ρ•sinθ,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
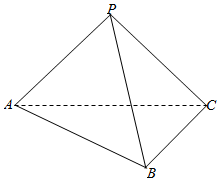 如图,在三棱椎P-ABC中,PA=PB=PC=AC=4,AB=BC=2$\sqrt{2}$.
如图,在三棱椎P-ABC中,PA=PB=PC=AC=4,AB=BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
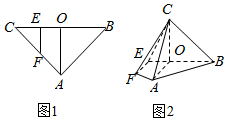 在等腰直角三角形ABC中(图1),斜边BC=6,O为BC的中点,E,F分别在OC和AC上,且EF∥AO,现将三角形以EF为折痕,向上折成60°的二面角,且使C在平面ABEF内的射影恰好为O点(图2)
在等腰直角三角形ABC中(图1),斜边BC=6,O为BC的中点,E,F分别在OC和AC上,且EF∥AO,现将三角形以EF为折痕,向上折成60°的二面角,且使C在平面ABEF内的射影恰好为O点(图2)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四边形ABCD为梯形,AB∥DC,对角线AC,BD交于点O,CE⊥平面ABCD,CE=AD=DC=BC=1,∠ABC=60°,F为线段BE上的点,$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{EB}$.
已知四边形ABCD为梯形,AB∥DC,对角线AC,BD交于点O,CE⊥平面ABCD,CE=AD=DC=BC=1,∠ABC=60°,F为线段BE上的点,$\overrightarrow{EF}$=$\frac{1}{3}$$\overrightarrow{EB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
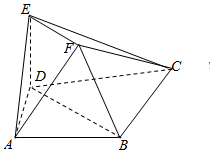 梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE=$\frac{1}{2}$BD,BD=BC=CD=$\sqrt{2}$AB=$\sqrt{2}$AD=2,DE⊥BC.
梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE=$\frac{1}{2}$BD,BD=BC=CD=$\sqrt{2}$AB=$\sqrt{2}$AD=2,DE⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{4}{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3),16 | B. | (-1,3),4 | C. | (1,-3),16 | D. | (1,-3),4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com