
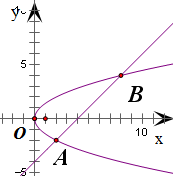
 由方程组
由方程组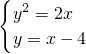 ,解之得
,解之得 或
或
 +
+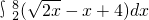
 =(
=( •
•
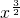 )
)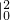 =
= ,
,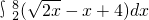 =(
=( •
•
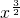 -
- x2+4x)
x2+4x)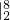
 •
• •
•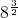 -
- ×82+4×8)-(
×82+4×8)-( •
• •
• -
- ×22+4×2)=
×22+4×2)=
 +
+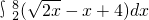 =
= +
+ =18
=18 在[0,2]上的积分值,与函数y=
在[0,2]上的积分值,与函数y= -(x-4)在[2,8]上的积分值之和.利用公式分别算出这两个积分的值,相加即得所求图形的面积.
-(x-4)在[2,8]上的积分值之和.利用公式分别算出这两个积分的值,相加即得所求图形的面积.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com