已知函数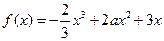
.
(Ⅰ)当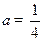
时，求函数
在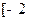
，
上的最大值、最小值；
(Ⅱ)令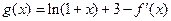
，若
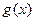在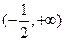
上单调递增，求实数
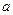的取值范围.
名校课堂系列答案科目：高中数学 来源： 题型：解答题
(本小题满分12分)
某厂家拟在2012年举行促销活动，经调查测算，该产品的
年销售量（即该厂的年产量）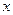
万件与年促销费用
万元（
（
为
常数），如果不搞促销活动，则该产品的年销售量只能是1万件．已知2012年生产该产品的
固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格
定为每件产品年平均成本的1.5倍（产品成本包括固定投入和再投入
两部分资金）．
(Ⅰ) 将2012年该产品的利润y万元表示为年促销费用万元的函数；
(Ⅱ) 该厂家2012年的促销费用投入多少万元时，厂家的利
润最大？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知f (x)＝ax－ln(－x)，x∈(－e,0)，g(x)＝－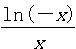
，其中e是自然常数，a∈R．
（1）讨论a＝－1时, f (
x)的单调性、极值；
（2）求证：在（1）的条件下，|f (x)|＞g(x)＋1/2；
（3）是否存在实数a，使f (x)的最小值是3，如果存在，求出a的值；如果不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(本小题满分13分）已知函数
的图象过点（1, -4),且函数
的图象关于y轴对称.
(1) 求m、n的值及函数
的极值；
(2) 求函数
在区间
上的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的对称轴为
,即
时，应有
，所以
时成立…………9分
,即
时，应有
即:
…………12分
分13分）已知
，函数
.
时讨论函数的单调性；
取何值时，
取最小值，证明你的结论.
，则
．
是角终边上一点,则
的值等于( )
是定义在R上的连续函数，且
，则
（ ）
在点
处连续，则常
的值是 （ ）
2 
3 
4 
5