
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
分析 根据正弦定理与三角恒等变换公式,化简题中的等式得到2sinBsinA=sinB,从而算出sinA=$\frac{1}{2}$,结合A的范围即可得解A的值.
解答 解:∵A+C=π-B,A,B∈(0,π),
∴sin(A+C)=sinB>0,
又∵2bsinA=acosC+ccosA,
∴2sinBsinA=sinAcosC+cosAsinC=sin(A+C)=sinB,
结合sinB为正数,可得sinA=$\frac{1}{2}$.
∵A∈(0,π),
∴A的值为$\frac{π}{6}$或$\frac{5π}{6}$.
故选:D.
点评 本题给出三角形满足的条件,求角A的大小,着重考查了利用正弦定理解三角形、三角恒等变换等知识,属于中档题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (-2,-1) | C. | (-1,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{24}$ | B. | $\frac{175}{132}$ | C. | $\frac{175}{264}$ | D. | $\frac{17}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∉R,总有x2+1>0” | B. | “?x∈R,总有x2+1≤0” | ||
| C. | “?x∈R,使得x2+1≤0” | D. | “?x∈R,使得x2+1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
设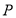 是椭圆
是椭圆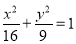 上的点,
上的点, 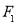 、
、 是椭圆的两个焦点,则
是椭圆的两个焦点,则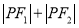 的值为( )
的值为( )
A. 10 B. 8 C. 6 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com