
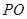 中,已知
中,已知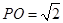 ,⊙O的直径
,⊙O的直径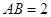 ,
,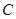 是
是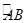 的中点,
的中点,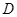 为
为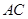 的中点.
的中点.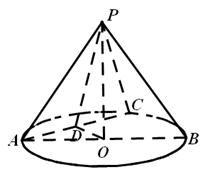
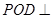 平面
平面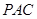 ;
;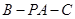 的余弦值.
的余弦值. 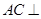 平面
平面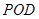 ,则可以根据面面垂直的判定定理来得到。
,则可以根据面面垂直的判定定理来得到。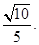
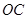 ,因为
,因为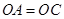 ,
,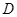 是
是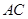 中点,所以
中点,所以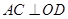
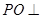 底面⊙O,
底面⊙O,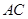
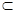 底面⊙O,所以
底面⊙O,所以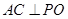 , 2分
, 2分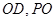 是平面
是平面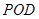 内的两条相交直线,所以
内的两条相交直线,所以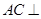 平面
平面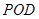 4分
4分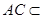 平面
平面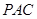 ,所以平面
,所以平面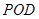
 平面
平面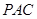 . 6分
. 6分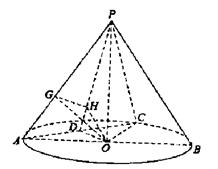
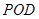 中,过
中,过 作
作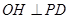 于
于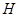 ,
, 平面
平面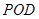
 平面
平面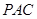 =
=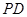
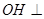 平面
平面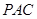 ,又
,又 面
面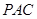 ,所以
,所以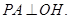
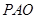 中,过
中,过 作
作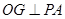 于
于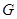 ,连接
,连接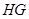 ,
,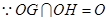
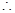
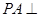 平面
平面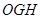 ,
,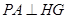 ,故
,故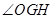 为二面角
为二面角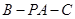 的平面角 9分
的平面角 9分

 在
在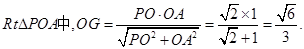
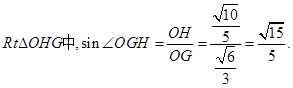
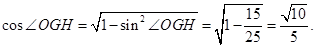 13分
13分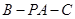 的余弦值为
的余弦值为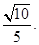 14分
14分 为坐标原点,
为坐标原点,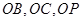 所在直线分别为
所在直线分别为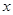 轴、
轴、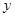 轴,
轴,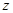 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则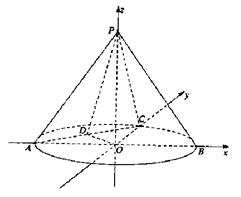
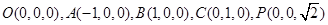 ,
, 2分
2分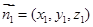 是平面
是平面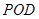 的一个法向量,
的一个法向量,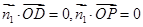 ,得
,得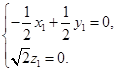
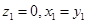 ,取
,取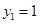 得
得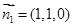 4分
4分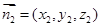 是平面
是平面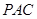 的一个法向量,
的一个法向量,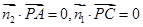 ,得
,得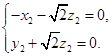
 ,取
,取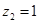 ,得
,得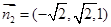 6分
6分 ,所以
,所以
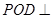 平面
平面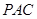 8分
8分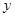 轴
轴 平面
平面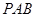 ,所以平面
,所以平面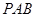 的一个法向量为
的一个法向量为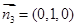
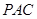 的一个法向量为
的一个法向量为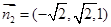
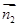 和
和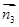 的夹角为
的夹角为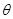 ,则
,则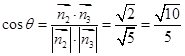 13分
13分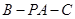 的余弦值为
的余弦值为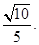 14分
14分

科目:高中数学 来源:不详 题型:解答题
 中,
中, ,
, ,
,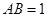 ,
, ,
, ,过
,过 作
作 ,垂足为
,垂足为 .
. 、
、 分别是
分别是 、
、 的中点.现将
的中点.现将 沿
沿 折起,使二面角
折起,使二面角 的平面角为
的平面角为 .
.

 平面
平面 ;
; 与面
与面 所成角的正弦值.
所成角的正弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的侧棱长为3,
的侧棱长为3, ,且
,且 ,
,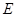 、
、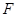 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且
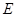 在何处,总有
在何处,总有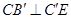 ;
; .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
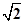 ,CD=CB=
,CD=CB=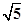 ,且
,且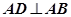 ,现将
,现将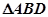 沿着对角线BD翻折成
沿着对角线BD翻折成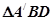 ,则在
,则在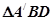 折起至转到平面
折起至转到平面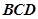 内的过程中,直线
内的过程中,直线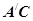 与平面
与平面 所成的最大角的正切值为( )
所成的最大角的正切值为( )| A.1 | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
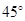 B.
B.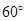 C.
C.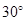 D.
D.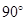
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
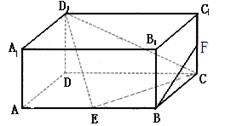
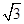 ,D、E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为 ( )
,D、E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为 ( )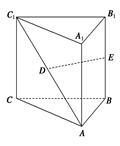
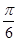 B.
B.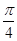 C.
C.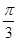 D.
D.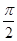
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com