
分析 可画出图形,由图形便可得到$\overrightarrow{AC′}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC′}$,从而由空间向量基本定理便可得出x,y,z的值,从而求出x+y+z.
解答 解:如图,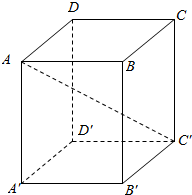
$\overrightarrow{AC′}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC′}$;
又$\overrightarrow{AC′}=x\overrightarrow{AB}+\frac{y}{2}\overrightarrow{BC}+\frac{z}{3}\overrightarrow{CC′}$;
∴由空间向量基本定理得:$\left\{\begin{array}{l}{x=1}\\{\frac{y}{2}=1}\\{\frac{z}{3}=1}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=3}\end{array}\right.$;
∴x+y+z=6.
故答案为:6.
点评 考查向量加法的几何意义,以及空间向量基本定理.


科目:高中数学 来源: 题型:解答题
 已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.
已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
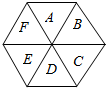 如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法?
如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>>0)点A(1,$\sqrt{2}$)是离心率为$\frac{\sqrt{2}}{2}$的椭圆C:上的一点,斜率为$\sqrt{2}$的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.
如图所示,已知$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>>0)点A(1,$\sqrt{2}$)是离心率为$\frac{\sqrt{2}}{2}$的椭圆C:上的一点,斜率为$\sqrt{2}$的直线BD交椭圆C于B、D两点,且A、B、D三点不重合.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com