|
|
|
数列{an}是等差数列,若a1+1,a3+3,a5+5构成公比为q的等比数列,则q=________.
|
|
|
答案:1
解析:
|
此题等差、等比数列为背景,考察方程思想、整体思想与换元法的运用.
|
练习册系列答案
相关习题
科目:高中数学
来源:人教B版(新课标) 必修1
题型:
|
|
|
下列函数中,在(0,+∞)上为减函数的是
|
| [ ] |
A. |
y=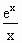
|
B. |
y=(1-x)ex
|
C. |
y=x3-x
|
D. |
y=x-ln(1+x)
|
|
|
查看答案和解析>>
科目:高中数学
来源:苏教版(新课标) 必修4
题型:
|
|
|
为得到函数y=cos2x的图像,只需将函数y=sin2x的图像
|
| [ ] |
A. |
向左平移 个长度单位 个长度单位
|
B. |
向右平移 个长度单位 个长度单位
|
C. |
向左平移 个长度单位 个长度单位
|
D. |
向右平移 个长度单位 个长度单位
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教A版(新课标) 选修4-2 矩阵与变换
题型:
|
|
|
定义运算: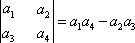 ,将函数 ,将函数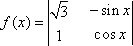 向左平移m个单位(m>0),所得图象对应的函数为偶函数,则m的最小值是_________. 向左平移m个单位(m>0),所得图象对应的函数为偶函数,则m的最小值是_________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
一个多面体的三视图如图所示,则该多面体的表面积为
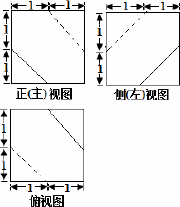
|
| [ ] |
A. |
21+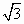
|
B. |
18+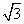
|
C. |
21
|
D. |
18
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记为比赛决出胜负时的总局数,求的分布列和均值(数学期望).
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
不等式组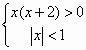 的解集为 的解集为
|
| [ ] |
A. |
{x|-2<x<-1}
|
B. |
{x|-1<x<0}
|
C. |
{x|0<x<1}
|
D. |
{x|x>1}
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6,0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买k台设备供甲、乙、丙、丁使用,若要求“同一工作日需使用设备的人数大于k”的概率小于0.1,求k的最小值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC= ,EA=2,∠ADE= ,EA=2,∠ADE= , ,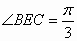
(1)求sin∠CED的值;
(2)求BE的长
|
|
|
查看答案和解析>>
