
(1)求证:如果一个平面经过一条线段的中点,那么这条线段的两个端点到平面的距篱相等;
(2)求证:空间四边形的两条对角线到这空间四边形各边中点所在平面的距离相等.
|
证明 (1)如图,O是线段AB的中点,且O∈平面α.
作 进而可以知道,若AB,AC,AD是空间不共面的三条线段,则A,B,C,D四点到线段AB,AC,AD的中点确定的平面的距离相等. (2)如图,设E,F,G,H依次是空间四边形ABCD的边AB,BC,CD,DA的中点,我们已证明E,F,G,H四点共面.
∵EF和EH分别是△ABC和△ABD的中位线, ∴AC∥EF,BD∥EH. ∵AC,BD都在平面EFGH外, ∴AC∥平面EFGH,BD∥平面EFGH. A到平面EFGH的距离就是AC到平面EFGH的距离,B到平面EFGH的距离就是BD到平面EFGH的距离. ∵平面EFGH经过AB的中点E,∴A,B到平面EFGH的距离相等. 故AC,BD到平面EFGH的距离也相等. 进而可以得到A,B,C,D到平面EFGH的距离也相等. 求距离是立体几何中一类重要的计算问题,在求解这类计算题时一般需要有三个步骤: (1)作图:即作出长度表示距离的线段; (2)证明:即证明所作线段的长就是所求的距离; (3)计算:根据已知条件计算出所作线段的长度得出所求的距离. |


科目:高中数学 来源:北京东城2000~2001学年度第二学期期抽测高一数学 题型:044
△ABC的三条边为a、b、c,其对角为A、B、C,如果2b=a+c,
(1)求证: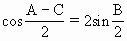 ;
;
(2)求:cosA+2cosB+cosC的值.
查看答案和解析>>
科目:高中数学 来源:2002年高中会考数学必备一本全2002年1月第1版 题型:044
设ABCD是矩形,沿对角线BD将△BDC折起,使C点在底面DAB内的射影H恰好落在AB边上(如图).
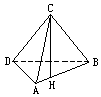
(1)求证:平面ABC⊥平面ACD;
(2)求证:平面DBC⊥平面ACD;
(3)如果AD∶AB=1∶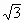 ,试求二面角C-AD-B的正弦值.
,试求二面角C-AD-B的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知函数f(x)=ln(1+x)-x1
(Ⅰ)求f(x)的单调区间;
(Ⅱ)记f(x)在区间![]() (n∈N*)上的最小值为bx令an=ln(1+n)-bx。
(n∈N*)上的最小值为bx令an=ln(1+n)-bx。
(ⅰ)如果对一切n,不等式![]() 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
(ⅱ)求证: ![]() 。
。
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(福建卷) 题型:选择题
(本小题满分14分)
已知函数f(x)=ln(1+x)-x1
(Ⅰ)求f(x)的单调区间;
(Ⅱ)记f(x)在区间 (n∈N*)上的最小值为bx令an=ln(1+n)-bx。
(n∈N*)上的最小值为bx令an=ln(1+n)-bx。
(ⅰ)如果对一切n,不等式 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
(ⅱ)求证:
 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com