
 如图所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1、AD1于点B1、P,作CC1∥AA1,分别交A1D1、AD1于点C1、Q,将该正方形沿BB1、CC1折叠,使得DD1与AA1重合,构成如图所示的三棱柱ABC-A1B1C1.
如图所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1、AD1于点B1、P,作CC1∥AA1,分别交A1D1、AD1于点C1、Q,将该正方形沿BB1、CC1折叠,使得DD1与AA1重合,构成如图所示的三棱柱ABC-A1B1C1. (BP+CQ)×BC=20.
(BP+CQ)×BC=20. SBCQP×AB=20.
SBCQP×AB=20.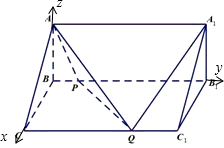
 =(0,3,-3),
=(0,3,-3),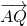 =(4,7,-3),
=(4,7,-3), =(x,y,z).
=(x,y,z). •
• =0,
=0, •
•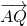 =0,即
=0,即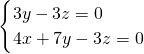 .
. =(-1,1,1).
=(-1,1,1). =(0,0,1).
=(0,0,1). ,
, >=
>=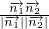 =
= .
.
 .
.

科目:高中数学 来源:2013-2014学年福建省福州市高三毕业班质检理科数学试卷(解析版) 题型:填空题
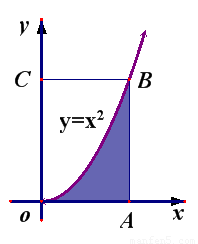
如图所示,在边长为1的正方形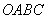 中任取一点
中任取一点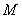 ,则点
,则点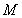 恰好取自阴影部分的概率为________.
恰好取自阴影部分的概率为________.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高三年级联考理科数学试卷(解析版) 题型:填空题
如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为________

查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省高三高考适应性考试理科数学试卷(一)(解析版) 题型:填空题
如图所示,在边长为1的正方形OABC中任取一点M.则点M恰好取自阴影部分的概率是 .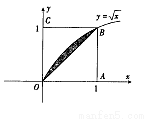
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(福建卷解析版) 题型:选择题
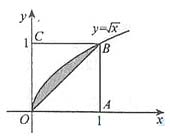
如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为
A、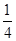 B、
B、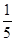 C、
C、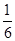 D、
D、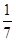
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com