
分析 由图象变换得到g(x)=2sin(4x+$\frac{π}{3}$),从而求函数的值域.
解答 解:将函数f(x)=6sin(2x+$\frac{π}{6}$)向左平移$\frac{π}{12}$个单位,
可得对应的函数解析式为:y=6sin(2(x+$\frac{π}{12}$)+$\frac{π}{6}$)=6sin(2x+$\frac{π}{3}$),
再将所的图象上各点的横坐标缩短为原来的$\frac{1}{2}$倍,纵坐标不变,
得到的图象对应的函数解析式为:y=6sin(4x+$\frac{π}{3}$),
则g(x)=6sin(4x+$\frac{π}{3}$),
∵0≤x≤$\frac{5π}{24}$,
∴0≤4x≤$\frac{5π}{6}$,
∴$\frac{π}{3}$≤4x+$\frac{π}{3}$≤$\frac{7π}{6}$,
∴-$\frac{1}{2}$≤sin(4x+$\frac{π}{3}$)≤1,
∴-3≤6sin(4x+$\frac{π}{3}$)≤6,
即g(x)在[0,$\frac{5π}{24}$]上的值域为[-3,6].
点评 本题考查了平面向量的数量积及三角函数的化简与其性质的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $±\frac{1}{9}$ | C. | $\frac{1}{3}$ | D. | $±\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
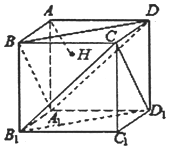 正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有以下四个命题:
正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有以下四个命题:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:选择题
一梯形的直观图是一个如图所示的等腰梯形,且梯形 的面积为
的面积为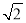 ,则原梯形的面积为( )
,则原梯形的面积为( )
A. B.
B.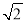 C.
C.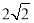 D.
D.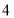
查看答案和解析>>
科目:高中数学 来源:2017届江苏南通市如东县等高三10月联考数学试卷(解析版) 题型:解答题
已知函数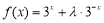
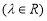
(1) 当 时,试判断函数
时,试判断函数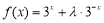 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2) 若不等式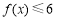 在
在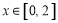 上恒成立,求实数
上恒成立,求实数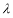 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com