
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,P为底面正方形ABCD内一个动点,Q为棱AA1上的一个动点,若|PQ|=2,则PQ的中点M的轨迹所形成图形的面积是( )
A.![]()
B.![]()
C.3
D.4π
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量 ![]() (件)与单价
(件)与单价 ![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(1)根据周销售量图写出 ![]() (件)与单价
(件)与单价 ![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润 ![]() (元)与单价
(元)与单价 ![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)其中ω>0,|φ|< ![]() .
.
(1)若cos ![]() cosφ﹣sin
cosφ﹣sin ![]() sinφ=0.求φ的值;
sinφ=0.求φ的值;
(2)在(1)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于 ![]() ,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象象左平移m个单位所对应的函数是偶函数.
,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象象左平移m个单位所对应的函数是偶函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|,a∈R. (Ⅰ)当a=2时,解不等式:f(x)≥6﹣|2x﹣5|;
(Ⅱ)若关于x的不等式f(x)≤4的解集为[﹣1,7],且两正数s和t满足2s+t=a,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示. 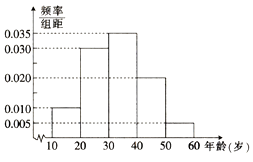
(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(2)若按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽的3人中,年龄在[40,50)以内的人数为X,求X的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lnx﹣mx+m.
(1)若f (x)≤0在x∈(0,+∞)上恒成立,求实数m的取值范围;
(2)在(1)的条件下,对任意的0<a<b,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知一艘海监船O上配有雷达,其监测范围是半径为25 km的圆形区域,一艘外籍轮船从位于海监船正东40 km的A处出发,径直驶向位于海监船正北30 km的B处岛屿,速度为28 km/h.
问:这艘外籍轮船能否被海监船监测到?若能,持续时间多长?(要求用坐标法)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某高中随机选取5名高一男生,其身高和体重的数据如表所示:
身高x(cm) | 160 | 165 | 170 | 175 | 180 |
体重y(kg) | 63 | 66 | 70 | 72 | 74 |
根据如表可得回归方程 ![]() =0.56x+
=0.56x+ ![]() ,据此模型可预报身高为172cm的高一男生的体重为( )
,据此模型可预报身高为172cm的高一男生的体重为( )
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com