
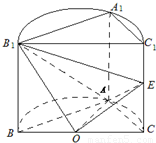
 如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4.
如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4.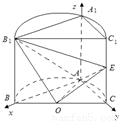 (I)证明:依题意可知,AA1⊥平面ABC,∠BAC=90°,如图建立空间直角坐标系A-xyz,因为AB=AC=AA1=4,则A(0,0,0),B(4,0,0),E(0,4,2),O(2,2,0),B1(4,0,4)
(I)证明:依题意可知,AA1⊥平面ABC,∠BAC=90°,如图建立空间直角坐标系A-xyz,因为AB=AC=AA1=4,则A(0,0,0),B(4,0,0),E(0,4,2),O(2,2,0),B1(4,0,4)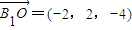 ,
,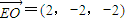 ,
,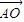 =(2,2,0)
=(2,2,0)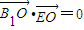 ,∴
,∴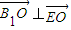
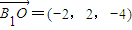 ,设平面B1AE的法向量为
,设平面B1AE的法向量为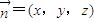 ,
,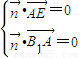 ,∴
,∴
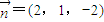
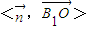 =
=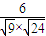 =
=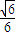
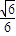 (8分)
(8分)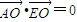 ,∴
,∴ ,∴AO⊥EO
,∴AO⊥EO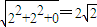 ,EO=2
,EO=2
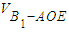 =
= S△AOE•B1O=
S△AOE•B1O=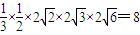 (12分)
(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
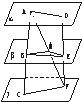 如图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,
如图,已知平面α∥平面β∥平面γ,且β位于α与γ之间.点A、D∈α,C、F∈γ,| AB |
| BC |
| DE |
| EF |
| h′ |
| h |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•青州市模拟)如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4.
(2012•青州市模拟)如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB面积的最大值是( )
(2012•石景山区一模)如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB面积的最大值是( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•滨州一模)如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8
(2013•滨州一模)如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com