
| 20 | 3 |
|
| 20 |
| 3 |
| 20 |
| 3 |
|
| 20 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013届辽宁省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
某商品定价为每件60元,不加收附加税时每年大约销售80万件,若政府征收附加税,每销售100元要征收 元(即税率为
元(即税率为 ),因此每年销量将减少
),因此每年销量将减少 万件.
万件.
(1)将政府每年对该商品征收的总税金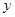 (万元),表示成
(万元),表示成 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2)要使政府在此项经营中每年收取的税金不少于128万元,问税率 应怎样确定?
应怎样确定?
查看答案和解析>>
科目:高中数学 来源:2010年重庆市高一12月月考数学试卷 题型:解答题
(12分)某商品定价为每件60元,不加收附加税时每年大约销售80万件,若政府征收附加税,每销售100元要征收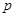 元(即税率为
元(即税率为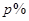 ),因此每年销量将减少
),因此每年销量将减少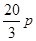 万件.
万件.
(1)将政府每年对该商品征收的总税金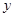 (万元),表示成
(万元),表示成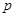 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2)要使政府在此项经营中每年收取的税金不少于128万元,问税率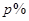 应怎样确定?
应怎样确定?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
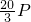 万件.
万件.查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆一中高一(上)12月月考数学试卷(解析版) 题型:解答题
 万件.
万件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com