
已知各项均为正数的数列 满足
满足 ,且
,且 ,其中
,其中 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 满足
满足 是否存在正整数m、n(1<m<n),使得
是否存在正整数m、n(1<m<n),使得 成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
(Ⅰ)数列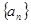 的通项公式为
的通项公式为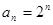
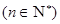 ;(Ⅱ)存在,
;(Ⅱ)存在,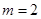 ,
,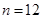 .
.
【解析】
试题分析:(Ⅰ)求数列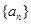 的通项公式,首先须知道数列
的通项公式,首先须知道数列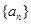 的特征,由题意
的特征,由题意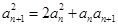 可得,
可得,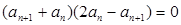 ,由于各项均为正数,故有
,由于各项均为正数,故有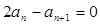 即
即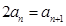 ,这样得到数列
,这样得到数列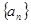 是公比为
是公比为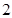 的等比数列,由
的等比数列,由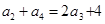 可求出
可求出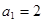 ,从而可得数列
,从而可得数列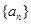 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列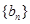 满足
满足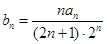 是否存在正整数
是否存在正整数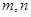
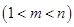 ,使得
,使得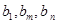 成等比数列,首先求出数列
成等比数列,首先求出数列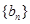 的通项公式,
的通项公式,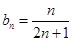 ,然后假设存在正整数
,然后假设存在正整数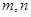
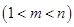 ,使得
,使得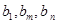 成等比数列,则
成等比数列,则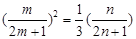 ,整理可得
,整理可得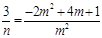 ,只要
,只要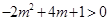 即可,解不等式求出
即可,解不等式求出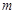 的范围,看是否有正整数,从而的结论.
的范围,看是否有正整数,从而的结论.
试题解析:(Ⅰ)因为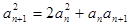 即
即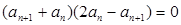
又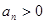 所以有
所以有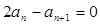 即
即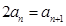
所以数列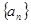 是公比为
是公比为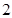 的等比数列
的等比数列
由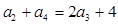 得
得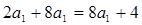 解得
解得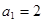 。
。
从而,数列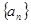 的通项公式为
的通项公式为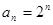
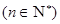 。
6分
。
6分
(II)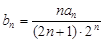 =
= ,若
,若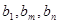 成等比数列,则
成等比数列,则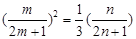 ,
,
即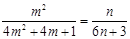 .
.
由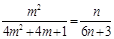 ,可得
,可得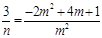 ,
,
所以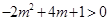 ,解得:
,解得: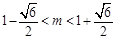 。
。
又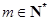 ,且
,且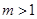 ,所以
,所以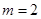 ,此时
,此时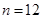 .
.
故当且仅当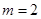 ,
,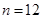 使得
使得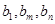 成等比数列。 13分
成等比数列。 13分
考点:等比数列的定义,及通项公式,探索性命题.


科目:高中数学 来源: 题型:
| Tn+1+12 |
| 4Tn |
| 2log2bn+1+2 |
| 2log2bn-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 与
与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
科目:高中数学 来源:青岛二模 题型:解答题
| Tn+1+12 |
| 4Tn |
| 2log2bn+1+2 |
| 2log2bn-1 |
查看答案和解析>>
科目:高中数学 来源:《第2章 数列》、《第3章 不等式》2010年单元测试卷(陈经纶中学)(解析版) 题型:解答题
 与
与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
科目:高中数学 来源:2012年高考复习方案配套课标版月考数学试卷(二)(解析版) 题型:解答题
 与
与 的大小,并加以证明.
的大小,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com